kolejność całkowania ola: jak zmienić kolejność całkowania?

	y2
∫dy( od −6 do 2) ∫f(x,y)dx (od		−1 do 2−y)
	4

prosze o pomoc

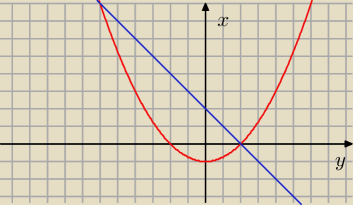
Krzysiek: i rozbij na sumę całek dla przedziałów: x∊[−1,0] i x∊[0,8]

ola: a czy y od −6 do 2 niczego nie ogranicza? ta figura to to załe pod niebieskim nad czerwonym po lewej ?

ola: czy ktoś by mógł to rozwiązać, bo nie umiem tego ogarnąć

Krzysiek: y∊[−6,2] mówi nam o tym,że liczymy pole figury na tym przedziale ale przecież moglibyśmy liczyć tylko pole np. dla y∊[−6,0].

ola: aha. ok dzięki bo dopiero zaczynam się uczyć i nie rozumiem

mateusz: up. próbuje przeanalizowac. i nie mogę pojąć schematu zmiany kolejności czy mógłby ktoś rozwiązać to zadanie krok po kroku, to dla mnie istotne zagadnienei na jutrzejsze kolokwium. a sam nie dam rady.

Krzysiek: to rozpiszę dla x∊[0,8] jak widać z rysunku kierując się zgodnie z osią 'y' (równolegle do osi y) w prawo najpierw przecinamy krzywą o równaniu: x=y²/4−1 ale że całkujemy po 'y' szukamy funkcji y=f(x) więc wyznaczasz 'y' z równania: x=y²/4−1 czyli: 4(x+1)=y² y=+/−2√x+1 z rysunku widzisz,że 'y' przyjmuje wartości ujemny więc jest to funkcja y=−2√x+1 następnie 'idąc dalej' przecinasz funkcję x=2−y czyli y=2−x więc granice całkowania to y∊[−2√x+1,2−x] ,x∊[0,8] dla x∊[−1,0] spróbuj Sam.

mateusz: thx Krzysiek! bardzo pomogłeś