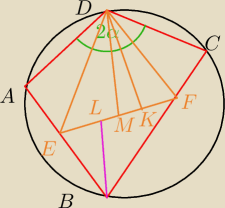
planim zawodus: Czworokąt ABCD wpisany jest w okrąg, przy czym |CD|=|DA|. Na odcinkach AB i BC wybrano odpowiednio punkty E i F, dla których ∡ ADC = 2∡ EDF. Odcinek DK jest wysokością trójkąta DEF, a DM jego środkową. Punkt L jest symetryczny do K względem M. Udowodnij, że proste DM i BL są równoległe.

kyrtap:

zawodus: Dzięki za rysunek A ktoś potrafi rozwiązać?

kyrtap:

bezendu: Na matematyka.pl też wiedzę dałeś

zawodus: To nie dla mnie, tylko dla koleżanki. Sam nie mam czasu pomyśleć, ale nie wiem czy bym to umiał

ZKS: http://archom.ptm.org.pl/?q=node/188

kyrtap: ja dzisiaj siedziałem godzinę nad tym zadaniem i ściana

zawodus: ZKS dzięki wielkie wiedziałem że to zadanie z olimpiady, ale nie wykorzystałem googla, bo myślałem że koleżanka to zrobiła Wystarczyło poszukać