symetria wzgedem prostej KGB: Witam, prosze o wytlumaczenie od podstaw tego zadania: Znajdz wzor funkcji g symetrycznej wzgeldem prostej y = x − 1do funkcji f, gdzie f(x) = x² − 4 To moje pierwsze zadanie tego typu, z checia przyjme wyjasnienie na innych ( prostszych ) przykladach, chyba ze ten wcale nie jest trudniejszy od innych

wredulus_pospolitus: 1) Musisz (ale to musisz) zrobić rysunek i narysować te dwie funkcje 2) Zauważ, że funkcja f(x) ma z prostą dwa punkty wspólne (to ważna informacja) 3) Funkcja symetralna to będzie funkcja 'odwróconego' względem tej prostej y=x−1 (to tak jak 'robienie' funkcji z wartością bezwzględną −−− tylko tam 'odbijasz symetralnie' jedynie część wykresu) 4) Tak więc wykresem g(x) także będzie parabola 5) Parabola ta będzie przecinała prostą y=x−1 w tych samych dwóch punktach co f(x) (punkt na prostej nie poruszy się przy 'odbijaniu') 6) Musisz jeszcze wyznaczyć nową współrzędną jakiegokolwiek punktu funkcji g(x) ... proponuje wyznaczyć współrzędne wierzchołka tej nowej paraboli 7) W tym celu −−− musisz obliczyć odległość wierzchołka paraboli f(x) od prostej y=x−1 (najlepiej od razu wyznacz prosta k prostopadłą do y=x−1 i przechodzącą przez ten wierzchołek 8) Na tej prostej k 'odkładasz' wyliczoną wartość z pkt 7 i masz juz współrzędne punktu wierzchołka paraboli g(x) 9) mając współrzędne trzech punktów jesteś w stanie wyznaczyć wzór funkcji g(x) koooniec opisu

KGB: Dzieki wielkie To teraz do pracy !

J: Hmm ...? Obawiam się,że to nie rozwiąże problemu... bez udziału programu komputerowego.

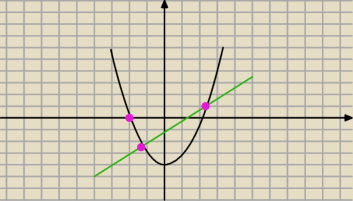
J: No i teraz rysujemy parabolę przechodząca przez te trzy punkty..

KGB: x − 1 = x² − 4 => x² − x − 3 = 0 (1)

	1 +/− √13
x1 / x2 =
	2

k: y = −x − 4 y = x − 1 y = −x − 4 2y = −5 => (x,y) = (−3/2 , −5/2 ) = S S = (W + W' )/2 =? W' = ( −3 , −1 ) f'(x) = a(x−x₁)(x−x₂) => y' = a(x² − x − 3) − przepisalem sobie z (1), moge tak zrobic ? f(−3) = −1 −1 = a ( 9+3−3) =9a

	−1
f(x) =		(x2 − x −3 ) ?
	9

J: I teraz narysuj sobie obydwie parabole w jednym układzie współrzędnych oraz prostą: y = x − 1

KGB: Ale ja potrzebuej tylko wzor, to ten wyzej wymieniony jest oK?

J: Namawia Cię narysuj ... a zobaczysz, co dostaniesz.

KGB: Jak rysuje, to nie za bardzo wychodzi parabola.

KGB: Za 2/3 godz. po obiadku na nowo sie wezme, dzieki za pomoc.

J: A no własnie ... szkoda było Twojej pracy i "wredulusa" , zobacz post:12:23

pigor: .. , Znajdź wzór funkcji g symetrycznej względem prostej y=x−1do funkcji f, gdzie f(x) = x2 − 4. −−−−−−−−−−−−−−−−−−−− o ile się gdzieś nie walnąłem, to g(x)= √x+1−3 − szukany wzór funkcji g.

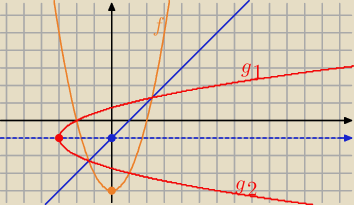
Bogdan: f(x) = x² − 4, oś symetrii y = x − 1 Jeśli przesuniemy układ współrzędnych o wektor [0, −1], to otrzymamy nowy układ współrzędnych, w którym f(x) przyjmie wzór h(x) = x² − 3, a oś symetrii wzór y = x. Wyznaczenie w pierwotnym układzie współrzędnych wzoru funkcji symetrycznej do funkcji f(x) = x² − 4 względem prostej y = x − 1 w nowym układzie współrzędnych z osią symetrii y = x sprowadza się do wyznaczenia funkcji odwrotnej do h(x) = x² − 3. Wyznaczamy funkcje odwrotne dla x∊(−∞, 0> oraz dla x∊<0, +∞). Dla x∊(−∞, 0>: y = x² − 3 ⇒ x² = y + 3 ⇒ x = −√y + 3, h⁻¹(x) = −√x + 3 Dla x∊<0, +∞): y = x² − 3 ⇒ x² = y + 3 ⇒ x = √y + 3, h⁻¹(x) = √x + 3 Wracamy do pierwotnego układu współrzędnych podnosząc nowy układ o wektor [0, 1]. Otrzymujemy szukane wzory dla funkcji g(x): g₁(x) = −√x + 3 − 1 oraz g₂(x) = √x + 3 − 1

Mila: Na pewno jest pomyłka, to ma być równanie krzywej .

Mila: Moja uwaga do wpisu Pigora.