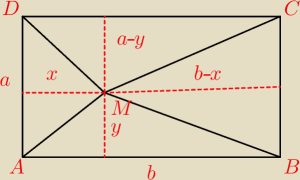
Zadanie z dowodzeniem spontan: Punkt M leży wewnątrz prostokąta ABCD. Udowodnij, że : |AM|² + |CM|² = |BM|² + |DM|². Jakieś rady ?

Lukas:

spontan: Dzięki wielkie, a jeszcze jedno zadanko mam. Na boku BE trójkąta ABC wybrano punkt D tak, by |kąt CAD| = |kątABC|. Odcinek AE jest dwusieczną kąta DAB. Udowodnij, że |AC| = |CE|

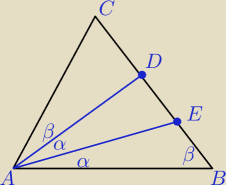
Lukas: <CAE=α+β <CEA=180−<AEB=α+β Są więc równe

spontan: Dzięki wielkie. Z dowodów nie jestem najlepszy ;\

Lukas: Ja też nie, dwa działy których nie znoszę to planimetria i logarytmy..

kyrtap: Planimetrię można wypracować robiąc zadania