Zagadnienia optymalizacyjne
Boa: 1) Z kawałka drutu o długości 60 cm wykonano prostokątną ramkę. ramka ta obracając się wokół
jednego z boków, zakreśla walec. a)Wyraź objętość walca jako funkcję zmiennej x, gdzie x to
promień podstawy walca i określ dziedzine. b)wyznacz wartość zmiennej x, dla której objętość
walca jest największa
2) W rogac prostokątnego arkusza blachy o wymiarach 36cm na 24cm wycieto cztery przystające
kwadraty i po zgięciu blachy otrzymano pudełko(bez górnej ścianki) o największej możliwej
objętości. oblicz wysokość pudełka.
28 maj 18:41
Janek191:
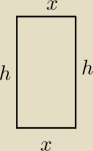
z.1
a)
2 x + 2 h = 60
x + h = 30
h = 30 − x
V = π x
2*h = π x
2*( 30 − x)
x ∊ ( 0 ; 30)
−−−−−−−−−−−−
28 maj 18:55
Janek191:
b) V(x) = 30π x2 − π x3
V'(x) = 60π x − 3π x2 = 0 ⇔ x*( 20 − x) = 0 ⇔ x = 20
V"(x) = 60π − 6π x
V"( 20) < 0
V jest największe dla x = 20.
=====================
28 maj 19:01
Boa: Janek a skąd się wziął wzór V(x)?
28 maj 19:07
Janek191:

V(x) = ( 36 − 2x)*( 24 − 2x)*x = ( 864 − 72 x − 48 x + 4 x
2)*x = 4 x
3 − 120 x
2 + 864 x
więc
V'(x) = 12 x
2 − 240 x + 864 = 0 ⇔ x
2 − 20 x + 72 = 0
Δ = 400 − 4*1*72 = 400 − 288 = 112 = 16*7
√Δ = 4
√7
| | 20 − 4√7 | |
x = |
| = 10 − 2√7 lub x = 10 + 2√7 ≈ 15,3 − odpada |
| | 2 | |
V" (x) = 2x − 20
V"( 10 − 2
√7) = 20 − 4
√7 − 20 = − 4
√7 < 0
Objętość pudełka jest największa dla x = 10 − 2
√7.
=====================================
28 maj 19:16
Janek191:
z.1
Wzór na objętość walca
V = Pp*h = π r2 *h
Ponieważ r = x oraz h = 30 − x
więc
V(x) = π x2*( 30 −x) = 30π x2 − π x3
================
28 maj 19:19
Janek191:
Wykorzystano I i II pochodną do wyznaczenia maksimum funkcji V(x)

28 maj 19:20
Boa: Dzięki bardzo


28 maj 19:24
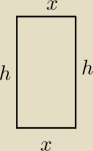 z.1
a)
2 x + 2 h = 60
x + h = 30
h = 30 − x
V = π x2*h = π x2*( 30 − x)
x ∊ ( 0 ; 30)
−−−−−−−−−−−−
z.1
a)
2 x + 2 h = 60
x + h = 30
h = 30 − x
V = π x2*h = π x2*( 30 − x)
x ∊ ( 0 ; 30)
−−−−−−−−−−−−
 V(x) = ( 36 − 2x)*( 24 − 2x)*x = ( 864 − 72 x − 48 x + 4 x2)*x = 4 x3 − 120 x2 + 864 x
więc
V'(x) = 12 x2 − 240 x + 864 = 0 ⇔ x2 − 20 x + 72 = 0
Δ = 400 − 4*1*72 = 400 − 288 = 112 = 16*7
√Δ = 4√7
V(x) = ( 36 − 2x)*( 24 − 2x)*x = ( 864 − 72 x − 48 x + 4 x2)*x = 4 x3 − 120 x2 + 864 x
więc
V'(x) = 12 x2 − 240 x + 864 = 0 ⇔ x2 − 20 x + 72 = 0
Δ = 400 − 4*1*72 = 400 − 288 = 112 = 16*7
√Δ = 4√7


