proszę o pomoc w rozwiązaniu tego zadania
kajlu : | | P(A') | | 1 | | 3 | |
Oblicz P(A) jezeli |
| = 3 wiedząc,że P(A') = |
| P(B') = |
| P(A∩B) = |
| | P(A) | | 3 | | 5 | |
Oblicz :
a) P(A∪B)
b) P(A'∩B')
c) P(A'∪B')
28 maj 17:29
kyrtap: | 1 − P(A) | |
| = 3 / * P(A) |
| P(A) | |
1 − P(A) = 3P(A)
4P(A) = 1/ :4
28 maj 18:38
kyrtap: P(A∪B) = P(A) + P(B) − P(A∩B)
| | 2 | | 2 | | 1 | | 40 + 24 − 15 | | 49 | |
P(A∪B) = |
| + |
| − |
| = |
| = |
| |
| | 3 | | 5 | | 4 | | 60 | | 60 | |
28 maj 18:42
kyrtap:
((
28 maj 18:49
kyrtap: To co na czerwono to P(A'∩B')
28 maj 18:50
kyrtap: Ω = (A ∪ B) ∪ (A'∩B') (z aksjomatu prawdopodobieństwa) ⇒
(A ∪ B) ∩ (A'∩B') = ∅
⇒ P(Ω) = P(A ∪ B) + P(A'∩B')
28 maj 18:58
kyrtap:
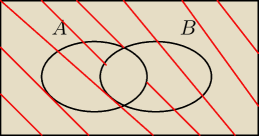
To co na czerwono to
P(A'∪B')
28 maj 19:01
kyrtap: Ω = (A'∪B') ∪ (A∩B) (z aksjomatu prawdopodobieństwa) ⇒
(A'∪B') ∩ (A∩B) = ∅
⇒ P(Ω) = P(A'∪B') + P(A∩B)
28 maj 19:04
kyrtap: to chyba wszystko
28 maj 19:04
kajlu : dzięki Ci bardzo
!
28 maj 19:58