W kwadrat o boku długości a wpisano koło, w które wpisano kwadrat, a w ten kwadr
Adam: W kwadrat o boku długości a wpisano koło, w które wpisano kwadrat, a w ten kwadrat znów koło
itd. Oblicz sumę:
a) obwodów;
b) pól
wszystkich kół.
27 maj 22:12
sushi_ gg6397228:
jedziesz z rysunkiem
liczysz dla 4 pierwszych i potem coś widziesz i zapisujesz sume
27 maj 22:16
Adam: obwód dla pierwszego bedzie 2πa/2 a promien drugiego koła jest równy ile? 2/3 pierwszego?
27 maj 22:22
sushi_ gg6397228:
jak nie zrobisz rysunku, to po co strzelasz lcizbami
27 maj 22:32
Hajtowy:
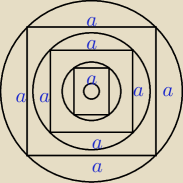
27 maj 22:36
Piotr:
kompletnie zly rysunek.
27 maj 22:41
pigor: ...cóż zakładam, że masz 2 kwadraty i dwa koła w nie wpisane
zgodnie z warunkami zadania i (o
n), (p
n) − ciągi geometryczne
obwodów i pól tych kół w których :
o1=2πr=2π*
12a=
πa i
p1=πr
2=π(
12a)
2=
14πa2, to
promień r
1 drugiego koła spełnia proporcję r
1 :
12a=
12a :
12]ap[2, skąd
r
1=
14√2a, stąd
o2=2πr
1=2π*
14√2a=
12π√2a i
p2=πr
12=
18πa2, więc
qo= o
2 : o
1=
12√2 − iloraz ciągu obwodów kół (dł.okręgów), zaś
qp= p
2 : p
1=
12 − iloraz ciągu pól powierzchni kół, zatem szukane
sumy obwodów i pól spełniających warunki zadania, to liczby :
| | o1 | | πa | |
a)So= |
| = |
| =U{2πa}{2−√2= πa (2+√2), |
| | 1−qo | | 1−12√2 | |
| | p1 | | 14πa2 | | πa2 | |
b)Sp= |
| = |
| = |
| = 12πa2. ...  |
| | 1−po | | 1−12 | | 2 | |
27 maj 23:33

