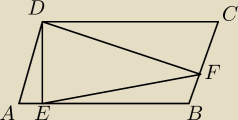
z rownloegloboku ABCD ( to ten rysunek) wysokosc DE ma dlugosc 24 cm , a sinus k Adam: z rownloegloboku ABCD ( to ten rysunek) wysokosc DE ma dlugosc 24 cm , a sinus kata EDF jest rowny 12/13 . Wiedzac ze pole trojkata DEF wynosi 1728/13 cm2 , oblicz a) dlugosc DF rownolegloboku b) dlugosci bokow i pole rownolegloboku ABCD (dfc i ard to kąty proste) punkt a zrobiłem ze wzoru 1/2 * a * b * sin a niestety punktu b nie moge zrobic. Pomożecie?

Adam: Da ktoś radę mi pomóc?

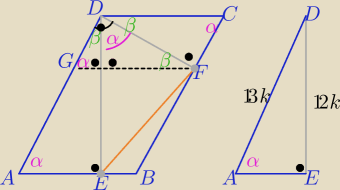Eta: |∡GDF|=|∡CFD|=90^o −−− jako kąty naprzemianległe to |∡BAD|=α

	12		12k
sinα=		=		to |DE|=12k=24 ⇒ k=2
	13		13k

to: |AD|=13k=26 =|BC| P(ABCD)= |DF|*|BC|= 12*26=312 cm²

pigor: ...lub |∡BAD|=|∡EDF|=α jako kąty o ramionach odpowiednio prostopadłych, wtedy ΔAED ∼ ΔCFD , więc a) |DF|= ¹₂*24=12, oraz

	24		12
b) z ΔAED:		=		⇒|AD|=26, to |CD|=12*26=13
	|AD|		13

więc pole równoległoboku ABCD= 26*12= . ...