współrzędne proszę o pomoc! : punkty B (2,0) i C (12,0) są wierzchołkami trójkąta prostokątnego ABC o przeciwprostokątnej BC. Wierzchołek A leży na prostej o równaniu y=x . Oblicz współrzędne punktu A

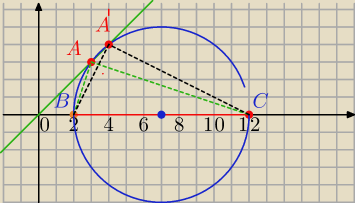
Mila: k: y=x A=(x,x) i BA⊥AC Srodek BC:

	2+12
S=(		,0)=(7,0)
	2

	1
Kreślimy okrąg o środku w punkcie s i promieniu r=		|BC|=5
	2

∡BAC=90^o jako wpisany w okrąg oparty na średnicy ∡BA'C=90^o jako wpisany w okrąg oparty na średnicy Znajdujemy wsp. punktów przecięcia okręgu i prostej (x−7)²+y²=5² y=x x²−14x+49+x²=25 dokończysz?

pigor: ..., punkty B (2,0) i C (12,0) są wierzchołkami trójkąta prostokątnego ABC o przeciwprostokątnej BC. Wierzchołek A leży na prostej o równaniu y=x . Oblicz współrzędne punktu A. −−−−−−−−−−−−−−−−−−−−−− lub np. tak: z warunków zadania A=(x,y)=(x,x)=? i AB=[2−x,−x], AC=[12−x,−x], wektory AB⊥AC ⇔ ABoAC=0 ⇔ [2−x,−x]o[12−x,−x]=0 ⇔ (2−x)(12−x)+x²=0 ⇔ ⇔ 24−14x+x²+x²=0 /:2 ⇔ x²−7x+12=0, stąd i z wzorów Viete'a ⇔ ⇔ x=3 v x=4 , a więc A=(3,3) lub A=(4,4) − szukany wierzchołek A.

Mila: No i tak nas olał. A prosi o pomoc.

pigor: ..., a ja już się na to... uodporniłem i nawet jest mi z tym dobrze, bo chociaż nie zawraca mi de...