Wykaż monotoniczność ciągu asiasiasia: wykaż, że ciąg ( a_n ) jest ciągiem rosnącym, jeśli: a) a_n = √3 +1 b) a_n = n+1 / n+3 c) a_n = n² − n − 2

5-latek: https://matematykaszkolna.pl/strona/263.html tak badasz monotonicznosc ciagu

Saizou : a) c. stały b,c) sprawdź a_n+1>a_n

asiasiasia: b) wyjdzie malejący? czy mam źle?

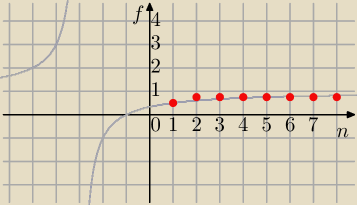
Mila: b) I sposób − wykres funkcji:

	n+1
f(n)=		i n∊N+
	n+3

Funkcja f(n) jest rosnąca dla n∊N₊, zatem a_n jest ciagiem rosnącym II sposób Badamy znak różnicy: a_n+1−a_n

	n+2
an+1=
	n+4

	n+2		n+1		(n+2)*(n+3)−(n+1)*(n+4)
an+1−an=		−		=		=
	n+4		n+3		(n+4)*(n+3)

	2
=		>0⇔ciąg an jest rosnący
	(n+3)*(n+4)