planimetria
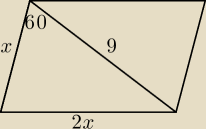
karol: oblicz obwód równoległoboku abcd wiedzac ze |AB|=2|AD| |BD|=9. kat ADB=60.
26 maj 17:00
razor: to chyba nie będzie prostokąt

26 maj 17:08
zawodus: no to nie moja sprawa

ten mi się najłatwiej rysowało

26 maj 17:11
karol: dzieki wielkie

26 maj 17:11
karol: ale x wychodzi 3 ?
26 maj 17:11
pigor: ..., czy taki "brzydki" obwód ma wyjść
9(√13−1) .

26 maj 17:24
zawodus: Pewnie ktoś wymyślił zadanie i nie patrzył na wynik

26 maj 17:26
pigor: ..., tw. cosinusów czy ...

na pewno dobrze zastosowałeś

26 maj 17:26
Bogdan:
| | 1 | |
Jeszcze raz: cos60o = |
| i x > 0 |
| | 2 | |
| | 1 | |
Z tw. cosinusów: 4x2 = 81 + x2 − 18x* |
| ⇒ x = ... |
| | 2 | |
26 maj 17:28
zawodus: Bogdan ma tę "władzę", że może sobie edytować

To od razu proszę o usunięcie moich postów z godziny 17.04 i 17.24, bo są bez sensu

26 maj 17:29
Bogdan:
zauważyłem

26 maj 17:29
karol: no moze taki wyjsc . bo mam pozniej zaokraglac. ..
26 maj 17:32
karol: na okregu opisano trapez prostokatny. odległosc środka okregu od konnców dłuzszego ramienia
wynosza 3 i 6 . oblicz promien okregu. pomozecie jeszcze z tym ?
26 maj 17:42
Bogdan:
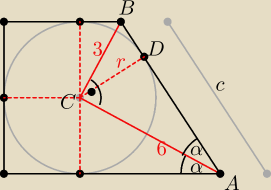
Szkic rozwiązania:
Trójkąt ABC jest prostokątny, CD jest wysokością tego trójkąta wychodzącą
z C i jednocześnie |CD| = r, gdzie r to długość promienia okręgu wpisanego w trapez.
c =
√32 + 62
26 maj 17:53
bezendu:
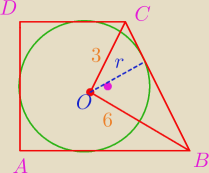
|OB|
2=3
2+6
2
|OB|=3
√5
P
OBC=9
0,5*r*3
√5=9
3
√5r=18
26 maj 17:57
karol: skad wiemy ze punkt c czy tamo ma 90 stopni?
26 maj 17:59
zawodus: punkt nie ma 90 stopni.
Kąt BOC ma 90 stopni
26 maj 18:01
Bogdan:
Spróbuj karolu sam niektóre fakty ustalić
26 maj 18:01
pigor: ..., np. tak : z własności stycznych do okręgu z punktów
B i C poza nim, odcinki OC i OB to dwusieczne kolejnych kątów
trapezu |∡ABC|=2α i |∡BCD|=2β ⇒
2β=180o−2α jako kąty
jednostronne dwóch prostych równoległych (tu podstaw trapezu)
przeciętych sieczną (tu ramię trapezu BC) , stąd dalej
β=90o−α,
więc w ΔBOC:
|∡BOC|=180
o−α−90
o+α=
90o . ...

26 maj 18:26
karol: dzieki

26 maj 18:35
Eta:
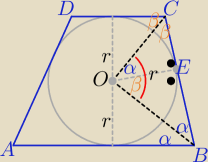
2α+2β=180
o ⇒ α+β=90
o
trójkąty BOE i OEC są podobne z cechy (kkk) (
to |∡BOC|=α+β= 90
o
więc trójkąt BOC jest prostokątny i to wszystko
Pozdrawiam
π...a 
26 maj 18:36
pigor: ..., a ...

miarę kąta
η ...

26 maj 18:44
pigor: .., a
π ...

...
η
26 maj 19:23
Eta:

26 maj 19:24

 ten mi się najłatwiej rysowało
ten mi się najłatwiej rysowało 



 na pewno dobrze zastosowałeś
na pewno dobrze zastosowałeś 

 To od razu proszę o usunięcie moich postów z godziny 17.04 i 17.24, bo są bez sensu
To od razu proszę o usunięcie moich postów z godziny 17.04 i 17.24, bo są bez sensu 

 Szkic rozwiązania:
Trójkąt ABC jest prostokątny, CD jest wysokością tego trójkąta wychodzącą
z C i jednocześnie |CD| = r, gdzie r to długość promienia okręgu wpisanego w trapez.
c = √32 + 62
Szkic rozwiązania:
Trójkąt ABC jest prostokątny, CD jest wysokością tego trójkąta wychodzącą
z C i jednocześnie |CD| = r, gdzie r to długość promienia okręgu wpisanego w trapez.
c = √32 + 62
 |OB|2=32+62
|OB|=3√5
POBC=9
0,5*r*3√5=9
|OB|2=32+62
|OB|=3√5
POBC=9
0,5*r*3√5=9


 2α+2β=180o ⇒ α+β=90o
trójkąty BOE i OEC są podobne z cechy (kkk) (
to |∡BOC|=α+β= 90o
więc trójkąt BOC jest prostokątny i to wszystko
Pozdrawiam π...a
2α+2β=180o ⇒ α+β=90o
trójkąty BOE i OEC są podobne z cechy (kkk) (
to |∡BOC|=α+β= 90o
więc trójkąt BOC jest prostokątny i to wszystko
Pozdrawiam π...a 
 miarę kąta η ...
miarę kąta η ...
 ... η
... η
