calki ciekawsky: ∫ cos³(arctan(x/2))/sin²(arctan(x/2))

ciekawsky: dx

rafaelo:

	2√x2+4
−
	x

ciekawsky: mozesz wytlumaczyc?

Godzio:

	x   cos(arctg( )   2
... =
	x   tg2(arctg( )   2

	x
arctg(		) = t
	2

x
	= tg(t)
2

	2
dx =		dt
	cos2t

	2cos(t)		2cos(t)
... = ∫		dt = ∫		dt
	tg2(t) * cos2(t)		sin2(t)

sin(t) = u cos(t)dt = du

	2du		2		2		2
∫		dt = −		+ C = −		+ C = −		+ C
	u2		u		sin(t)		x   sin(arctg( ))   2

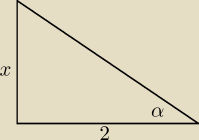
	x		x
tg(α) =		⇒ α = arctg(		) (patrz rys)
	2		2

	x
sin(α) =
	√x2 + 4

Stąd

	2√x2 + 4
... = −		+ C
	x

rafaelo:

	x   cos3(arctan( ))   2
∫		dx
	x   sin2(arctan( ))   2

∫a*f(x)dx= a*∫f(x)dx

	1
4∫
	x2   x2√ +1   4

	2
4∫		dx
	x2√x2+4

∫a*f(x)dx=a*∫f(x)dx

	1
4*2∫		dx
	x2√x2+4

	x2		x2		x
teraz x2+4=4(		+1) oraz oraz		= (		)
	4		4		2

	1
4*2∫		dx
	x   x2√4(( )2+1   2

	x		1
póżniej ∫f(g)(x))*g(x)dx=∫f(u)du, u=g(x) a u =		oraz du=		dx,
	2		2

dx=2du następnie ∫a*f(x)dx=a*∫f(x)*dx ∫f(g(x))*g(x)dx = ∫f(u)du, u=g(x) i skończ teraz proste operacje na całkach