Wartość bezwzględna Dawid: 3x−|x +1|=x+4 1. x+1≥0 x≥−1 3x−x+1=x+4 x=3 2. x+1<0 x<−1 3x+x−1=x+4

	5
x=
	3

Gdzie popełniłem błąd? Bo rozwiązaniem powinna być liczba 5 Dziękuje za pomoc

Piotr 10: 3 x − (x+1) = x+ 4 3x − x − 1= x+4

Piotr 10: 2 przypadek x < − 1 3x − ( −x −1) = x+4 3x+x +1=x+4 3x = 3 x=1 ∉D JEŚLI MASZ MINUS PRZED NAWIASTEM TO ZMIENIASZ ZNAK

Dawid: To wartość bezwzględna zamienia się w nawias ?

J: W drugim też żle ... 3x + x + 1

J: Dla x < − 1 I x+1 I = (− x − 1)

Piotr 10: Jeśli masz minus przed wartoscia bezwzgledna to bierz w nawias, mozesz to zrobic tez w pamieci

Dawid: To chyba lepiej jak przekształcę równanie do |x+1|=2x−4

Piotr 10: Oczywiście najlepiej redukcja wyrazow podobnych i dopiero opuszczasz WB

J: Dokładnie..., tak jak napisał Dawid ... najprostszy sposób, bez żadnych przedziałów.

Dawid: Rozumiem dziękuje .

Piotr 10: Możesz teraz podniesc do kwadratu obustronnie i zalożenie 2x − 4 ≥0

J: Po co ? ⇔ x+1 = 2x − 4 lub x+1 = −2x + 4 ... i po temacie.

Dawid: J to dlaczego tutaj nie jest rozwiązane takim sposobem jak podałeś ? https://matematykaszkolna.pl/strona/1109.html

Dawid: x+1 = 2x − 4 lub x+1 = −2x + 4 x=5 lub x=1 a ma być jedno rozwiązanie

J: Bo nie podał prostszej metody ... ⇔ 2x − 6 < x + 3 < 6 − 2x

op: 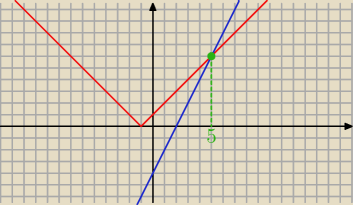y=|x+1| y=2x−4 rozwiązanie

J: Bo jeśli masz równanie: Ix+1I = 2x − 4 , to musisz zrobić dodatkowe założenie : 2x − 4 ≥ 0 ⇔ x ≥ 2 ... i dlatego rozwiązanie x = 1 odpada.