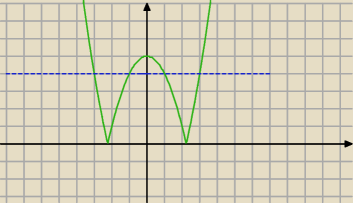
F.kwadratowa Lukas: Szkicując wykres funkcji rozwiąż nierówność a) |x²−5|>4 Jak odczytać z wykresu ?

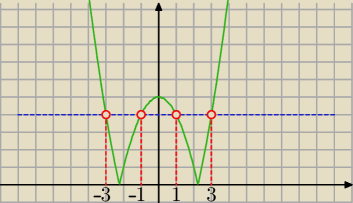
Domel: No dla jakich x−ów masz wykres nad niebieską linią

Eta: x∊(−∞,−3)U(−1,1)U(3,∞)

Domel: Witam Eta ciekawe czy Lukas też do tego doszedł

Eta: Witam Domel .......a no ciekawe?

Lukas: Witam Już teraz tak Domelku Dziękuję

Eta:

Lukas: Nie wiedziałem, że to tak się czyta Ale teraz już wiem

Eta:

Lukas: Jeszcze jak jesteś na forum to kilka wskazówek Mam funkcje daną wzorem f(x)=x²+2x+c wyznacz te wartości wsp c dla których wierzchołek paraboli, będącej wykresem funkcji f należy do paraboli y=2x²−7x+1 W=(x_w,2x²−7x+1) Jak to zacząć ?

Eta:

	−2
xw=		=−1 , yw=f(xw)= ........... = c−1 ⇒W(−1,c−1)
	2

teraz podstaw za x=−1 i y=c−1 do paraboli y=2x²−7x+1

Lukas: Ok, wyszło poprawnie.

Eta:

Lukas: Wykaż, że jeśli funkcje f(x)=x²+px+q i g(x)=x²+qx+p gdzie p≠q mają wspólne miejsce zerowe to p+q=−1 x²+px+q=x²+qx+p px+q−gx+p px−qx=p−q x(p−q)=p−q x=1 I dalej nie wiem co ?

Eta: x_o=1 ⇒ f(1)=0 i g(1)=0 ⇒ ......

Lukas: Ale tam mam p+q=−1 ?

Eta: f(1)=1+p+q=0 ⇒..... g(1)= 1+q+p=0 ⇒...... teza

Lukas: Dziękuję, świetnie tłumaczysz !

Eta:

Lukas: Ostatnie już na dzisiejszą noc: Wykaż, że dla dowolnych liczb rzeczywistych a,b,c funkcja f(x)=(x−a)(x−b)+(x−b)(x−c)+(x−c)(x−a) ma co najmniej jedno miejsce zerowe f(x)=3x²−2(b+a+c)x+ab+bx+ac Ale co mi to dało ?

Eta: f(x) = 3x²−2(a+b+c)x +ab+bc+ac warunek Δ≥0 .........

Lukas: I to wystarczy ? Dokończę jutro, dobranoc.

Eta: Miłych snów nie tylko o matematyce

Lukas: Raczej nastawiam się na ciężką pracę zaczynam więcej rozumieć i to mnie cieszy