Równanie symetralnej odcinka Tomasz: Symetralna − Proszę o sprawdzenie. 1. Napisz równanie symetralnej odcinka AB, jeśli A =(−3;4) i B=(0;7) Używam metody przez układ równań y = ax+b 4=−3a+b 7=0a+b a=1 Liczę środek odcinka AB:

	−3		4+7
S= [		,		]
	2		2

	1		1
S= [1		, 5		]
	2		2

współczynnik kierunkowy a*a1=−1 1*a1=−1 a1=−1 Podstawiam dane i liczę symetralną y = ax+b

	1		1		1		1
5		=−1*1		+b ⇒ 5		=−1		+b ⇒ b = 7
	2		2		2		2

równanie symetralnej ⇒ y=−1x+7 Dobrze ?

ja: ok

razor: Środek odcinka źle

ICSP: Czyli chcesz mi powiedzieć, że symetralna odcinka AB przechodzi przez punkt B Do poprawny.

PW: Każdy punkt P = (x,y) na symetralnej ma tę własność, że |PA| = |PB|. Zapisujemy to za pomocą współrzędnych i odpowiedź gotowa. Nie trzeba liczyć środka odcinka ani pisać równania prostej przechodzącej przez A i B.

Tomasz: Nie wiem gdzie zrobiłem błąd. Może ktoś naprowadzić ?

Tomasz: PW − Czym jest punkt P ?

ja:

	−3		1
Srodek dobrze policzyłas , tylko źleprzepisałaś		=−1
	2		2

Tomasz: Czyli w końcu zadanie jest poprawnie rozwiązane, czy nie ? Przyznam szczerze, że nie miałem nigdy Planimetrii i wszystkiego dzisiaj uczyłem się sam, także chciałbym wiedzieć czy dobrze rozumiem jak to się robi.

5-latek:

	−3
Tu ,		= −1,5 a nie 1,5
	2

Eta:

ja: Myślisz prawidłowo , tylko popraw ten błąd!

PW:

	3		1
Z −		zrobiłeś 1		.
	2		2

	11		1
A powiedz mi − czemu służy takie zamienianie , że na przyklad		= 5		? Chyba żeby
	2		2

się prędzej pomylić? Tak liczą dzieci w podstawówce, bo im łatwiej odejmować części całkowite osobno o ułamkowe osobno, ale już przy mnożeniu mamy koszmar. Odzwyczaj się od tego głupiego zapisu.

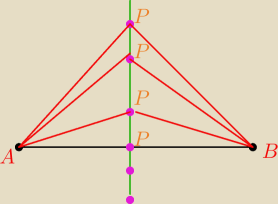
5-latek: Zielona to symetralna

Eta: S(−1,5 ; 5,5)

	7−4
wsp. kier AB : aAB=		= 1
	0+3

	1
symAB ⊥AB to sym AB: y= −		(x−xS)+yS
	aAB

y=−(x+1,5)+5,5 ⇒ y=−x+4

Tomasz: już widzę.

	1		1
5		= −1*(−1		) +b ⇒b = 4
	2		2

równanie symetralnej y= −1x+4, tak ?

PW: |AP|² = (x+3)² + (y−4)² |BP|² = (x−0)² + (y−7)² |AP| = |BP| ⇔AP|² = |BP|² ⇔ (x+3)² + (y−4)² = (x)² + (y−7)² ⇔ x²+6x+9 + y²−8y+16 =x²+y²−14y+49 ⇔ 6x+25 − 8y = −14y + 49 ⇔ 6y = − 6x + 24 ⇔ y = −x + 4. Nic nie umiem, tylko wzór na odległość punktów.

Tomasz: Dzięki za zainteresowanie.

Eta: