F.kwadratowa...
Lukas:
Funkcja y = (m + 1)x
2 − (2m + 4)x− 7 jest malejąca w zbiorze (−
∞ ;4) i rosnąca w zbiorze
(4;+
∞ ) . Wyznacz parametr m .
Wyznacz wszystkie wartości parametru m , dla których funkcja f (x) = (m
2 − 1)x
2 − 2mx + 4m +
5 jest rosnąca w przedziale (−
∞ ;1) i malejąca w przedziale (1;+
∞ )
| | 2m | |
a tutaj oprócz |
| =1 trzeba jeszcze coś ? |
| | 2(m2−1) | |
Od czego to zależy ?
23 maj 19:32
Saizou :
a co ze współczynnikiem a
23 maj 19:35
Eta:
Dodatkowo:
zad1/ m≠−1
zad2/ m≠ −1 i m≠1
23 maj 19:36
Lukas:
wiem, że do pierwszego m≠−1 bo to dziedzina wyrażenia wymiernego.. Ale zadałem inne pytanie ?
23 maj 19:43
Eta:
warunki ok

23 maj 19:45
Lukas:
No własnie nie ok

bo w drugim zadaniu wychodzą dwa wyniki a w odpowiedzi jest tylko jeden
wynik.
23 maj 19:49
Saizou :
a jaki musi być współczynnik kierunkowy, dodatni czy ujemny ?
23 maj 19:58
Lukas:
to nie ma znaczenia czy dodatni czy ujemny.
23 maj 20:02
Saizou :
Wyznacz wszystkie wartości parametru m , dla których funkcja f (x) = (m2 − 1)x2 − 2mx + 4m +
5 jest rosnąca w przedziale (−
∞ ;1) i malejąca w przedziale (1;+
∞ )
ja bym dał warunki
1
o m
2−1<0
m
2<1
lml<1
m∊(−1:1)
−m
2+m+1=0
Δ=1+4=5
23 maj 20:11
Lukas:
No i czytałeś wyżej to co napisałem ? Tutaj dajemy założenie odnośnie wsp.kierunkowego a w
przykładzie wyżej nie... i dlaczego tak jest ? Nie chodziło mi o rozwiązanie.
23 maj 20:14
Saizou : ale w tym pierwszym też powinno być założenie co do współczynnika a
23 maj 20:15
Piotr 10: musi być założenie co do wspólczynnika 'a'
23 maj 20:18
Lukas:
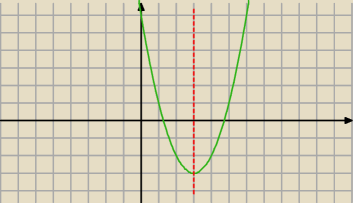
f(x)=x
2−6x+6
23 maj 20:26
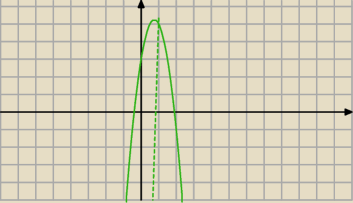
Lukas:
23 maj 20:27
Saizou : i czemu ma to dowodzić ?
23 maj 20:30
Lukas:
jeśli xw=1 to nie zależnie czy a<0 czy a>0
23 maj 20:33
Lukas:
tylko drugi rysunek trochę do bani
23 maj 20:34
Saizou : ale masz podane przedziały kiedy funkcja rośnie i maleje dlatego musi być założenie co do 'a'
23 maj 20:34
razor: A czy jeśli xw = 1 to funkcje będą rosnąć i maleć na tych samych przedziałach niezależnie od
a?
23 maj 20:34
Lukas:
Ok, już zrozumiałem. Ale robiąc pierwsze zadania bez badania wsp a wynik wyszedł prawidłowy

23 maj 20:41
Saizou :
bo w pierwszym jest tylko jedno rozwiązanie

ale mogłoby ono nie należeć do dziedziny i nie było by rozwiązania xd
na całe szczęście należy do dziedziny, btw brak dziedziny −1 ptk

23 maj 20:43
Lukas:
Uważam, że głupi ma zawsze szczęście

23 maj 20:55

 bo w drugim zadaniu wychodzą dwa wyniki a w odpowiedzi jest tylko jeden
wynik.
bo w drugim zadaniu wychodzą dwa wyniki a w odpowiedzi jest tylko jeden
wynik.
 f(x)=x2−6x+6
f(x)=x2−6x+6


 ale mogłoby ono nie należeć do dziedziny i nie było by rozwiązania xd
na całe szczęście należy do dziedziny, btw brak dziedziny −1 ptk
ale mogłoby ono nie należeć do dziedziny i nie było by rozwiązania xd
na całe szczęście należy do dziedziny, btw brak dziedziny −1 ptk 
