pomocy ola: narysuj wykres funkcji y=2(x−1)²+3

Radek: W czym problem ? Masz tutaj postać kanoniczną z której odczytasz wierzchołek funkcji. Potem sprowadź do postaci ogólnej i wylicz detle oraz x₁ i x₂

Radek:

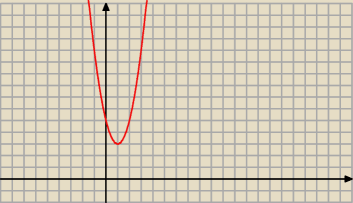
Radek: Delta < 0 nie ma miejsc zerowych więc odczytujesz współrzędne wierzchołka W=(1,3) Sprowadzamy do postaci ogólnej 2x²−4x+5 z współczynnika c odczytamy miejsce przecięcia z osią OY (0,5)

ZKS: Radek powiedz mi, po co liczyć Δ jak z postaci kanonicznej widać jak Δ wygląda? y = a(x − x_w) + y_w

	b
xw = −
	2a

	Δ
yw = −
	4a

u nas a = 2 , x_w = 1 oraz y_w = 3, więc

	Δ
−		= 3
	4 * 2

Δ = −24. Czyż nie? Dodatkowo widać, że ta funkcja nie ma miejsc zerowych, ponieważ 2(x − 1)² jest nieujemne, a dodając do tego liczbę dodatnią otrzymamy wyrażenie dodatnie, zatem wyrażenie 2(x − 1)² + 3 nigdy nie osiągnie w zbiorze liczb rzeczywistych wartości równej 0.

asdf: @ZKS czemu sie dziwisz? tak ucza w szkolach...daja uniwersalne rozwiazanie, zeby uczniowie dostali pkt na egzaminie, a nie zeby zrozumiec

PW: Podejście "szkolne" jest takie: Bierzemy funkcję kwadratową (ten wykres znamy, umiemy go narysować i nazwać) g(x) = 2x². Po przesunięciu jej wykresu o wektor [1, 3] otrzymamy wykres funkcji f(x) = 2(x−1)² + 3 Nic nie trzeba liczyć, jest to zadanie na zastosowanie twierdzenia o postaci funkcji powstałej w wyniku przesunięcia znanego wykresu o znany wektor.

asdf: uczniowie zganiaja na to, ze maja slabo wytlumaczone nauczycielka zgania na to, ze za malo czasu by wszystko wytlumaczyc dyrektor zgania na to, ze nie moze dac wiecej godzin, bo kasy juz na to nie ma

ola: to ja juz nic nie rozumiem wiem ze kazala mi do tego robic tabele i ze y czy cos tam równa sie 2x

PW: Rada gminy zgania na ministerstwo, że kiepski algorytm dotacji oświatowej. Jednym słowem wszyscy są zgonieni, tylko my tu powolutku i za darmo tłumaczymy jak chłop krowie.

PW: Do żalu z 15:00: − dobrze kazała. Najpierw rysujemy y=2x², tabelką jak to na początku nauki. x₁ = 0 ⇒ y₁ = 2•0² = 0 x₂ = 1 ⇒ y₂ = 2•1² = 2 x₃ = −1 ⇒ y₃ = 2•(−1)² = 2 i można tak dłużej i więcej, ale usypiam. Potem przesuwamy ten wykres o wektor [1, 3]. Jeżeli tego jeszcze nie było (nie wiesz o o idzie, a dopiero zaczynasz naukę o funkcji kwadratowej), to można od razu tworzyć tabelkę dla funkcji y = (x−1)³+3.

PW: Poprawka: y = (x−1)² +3, sąsiednie klawisze.