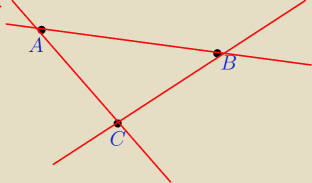
Linie proste 5-latek: Obieramy 3 punkty niewspolliniowe . Przez kazde dwa punkty prowadzimy linie prosta . Ile bedzie tych prostych i w ilu co najwyzej punktach przetna sie te proste . Otoz wiemy z eprzez dwa punkrty przechodzi tylko jedna prosta wiec tutaj bedzie tak : 3 proste i w 3 punktach punktach sie przetna co najwyzej

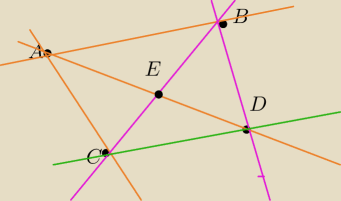
5-latek: Teraz mamy 4 punkty z ktorych zadnme 3 nie sa wspoliniowe . To samo polecenie Wiec tutaj mamy: 6 prostych i czy beda 4 punkty przeciecia czy tez nalezy policzyc takze punkt E ?

5-latek: Za szybko wyslalem . I czy jest na to jakis wzor ktory to okresla ?

zawodus: Robiłem coś na dyskretnej podobnego do tego Chyba będzie tutaj rekurencja

5-latek: Czesc . Sa to zadanka z geometrii Janowskiego do klasy 1 technikum (ucze sie sam Chyba mnie gosciu oszukal na alllegro bo zamowilem ksizake z geometrii do klasy 4 (Janowskiego i ani ksiazki od 7 maja ani kasy

zawodus: To lipa. Napisz do niego, a jeśli ci nie wyśle to daj mu komentarz na allegro. Komentarza nie da się usunąć

5-latek: Juz napisalem 2 razy i nie odpowiada a logowal sie ostatnio 18 maja

jakubs: Zgłoś sprawę do allegro.

5-latek: i tak zaraz zrobie (wiesz to nieduza kwota 14,50 zl ale zawsze to moja zarobiona kasa

zawodus: Choćby sprawa dotyczyła złotówki, to jest zwykła nieuczciwość...

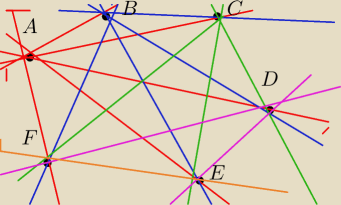
5-latek: Teraz mamy 6 roznych punktow i naliczylem ze przez 6 roznych punktow przechodzi 15 prostych

	n(n−1)
To wobec tego przez n roznych punktow przechodzi		prostych .
	2

A jak z punktami przeciecia ? Moglby ktos wytlumaczyc ?

5-latek: Wedlug aksjomatu dwie proste maja ablbo jedn punkt przeciecia albo wcale . Albo juz jesten na to z a stary albo .....

PW: Punktów przecięcia będzie więcej − zawęziłeś rysunek do pewnego "kadru", to się nie zmieściły. Nie ma np. punktu wspólnego prostych AC i BD. Każde dwie spośród sześciu mają punkt wspólny. A rysunek nie spełnia założeń zadania − punkty A, E i D są współliniowe, podobnie C, E i B.

PW: A, uszanowanie. Nie widziałem ostatniego rysunku, mój komentarz dotyczył ilustracji z 09:49.

5-latek: WItaj PW No tyle sie zmiescilo . Wedlug mnie te punkty co podales nie sa wspolliniowe gdzyz nie leza na jednej prostej . np punkty AED . jesli sie myle proszse narysuj odpowiedni rysunek . Wroce z pracy to bede analizowal .

5-latek: No wyjasnilo sie

PW: Poprawne rozwiązanie nie obędzie się bez dyskusji liczby prostych równoległych. Każde trzy punkty mają być niewspółliniowe, ale to nie znaczy, że nie mogą tworzyć prostych równoległych. Jeżeli jest w poleceniu "ile co najwyżej", to takiej trudnej dyskusji nie musimy prowadzić − zakładamy, że żadne dwie utworzone proste nie są równoległe, czyli przecinają się każde dwie dowolnie wybrane. W ten sposób uzyskamy odpowiedź na pytanie "ile co najwyżej", nic nie musimy rysować, bo zwariujemy.

5-latek: PW a czy jest jakis wzor ilosc punktow przeciecia ?

PW: Jeżeli dowolnie wybrane dwie mają punkt przecięcia, to jest tych punktów tyle, na ile sposobów można wybrać dwa elementy spośród k, gdzie k jest liczbą prostych (ten sam wzór, który już podawałeś, tylko tym razem stosowany do liczby k). Mówiłem, że książka Janowskiego jest dobra − stawia proste, ale niebanalne pytania i bardzo dobrze opowiada teorię.

5-latek: Podziekowac Jutro mam wolne wiec jescze sobie porysuje

	15*14
czyli jesli jest 15 prostych to bedzie		=105 punktow przeciecia co najwyzej
	2

5-latek: Jest wlasnie tak jak piszsez . NIby proste ale ....

kochanus_niepospolitus: 5−latek ... taka mała sprawa −−− ilość przekątnych + boków w wielokącie wypukłym = ilość tych właśnie prostych Zauważ jak rozmieszczone mają być te punkty ... a jak rozmieszczone są wierzchołki wielokąta wypukłego. Wniosek: wierzchołki wielokąta wypukłego są szczególnym przypadkiem rozmieszczenia punktów zgodnie z poleceniem zadania.

5-latek: dziekuje za wskazowke Artur Wszystko to jutro juz zapiszse sobie w notatkach

Piotr: Artur ? To Artur z pewnego miasta nad morzem ?

PW: Od początku tak podejrzewałem − zniknął Artur z miasta Neptuna, a pojawił się wredulus_ pospolitus, w chwilach lepszego humoru kochanus₋niepospolitus.

Piotr: pasuja tez znaki −−−

5-latek: czesc Piotr tak i jeszce wredulus_pospolitus

Piotr: czesc 5−latek dobrze widziec

5-latek: Jutro beda nastepne zadanka bo musze to od poczatku dobrze zrozumiec