Prosze o Pomoc Monika: Czy mógłby mi ktoś pomóc rozwiązac pare zadanek które własnie otrzymałam na jutrzejszy egzamin ja nie dam rady sama boje sie ze popełnie bład i z tym błędem będe sie uczyła .Jeszcze mam jutro kilka egzaminów ,dzieci i inne obowiązki licze na wasza pomoc była bym bardzo wdzieczna tylko ze mam te zagadnienia na zdj z aparatu a tu ich nie moge wstawic

Monika: moze e−mailowo byłby ktoś w stanie mi pomóc..

J: Spróbuj je napisać

Monika: http://zadane.pl/zadanie/7218356 tu są te zagadnienia bo na zadane wrzuciłam

J: Zad4) Funkcja róznowartościowa to taka funkcja, która dla dowolnych dwóch argumentów należących do dziedziny przyjmuje dwie różne wartości: ∀x₁,x₂ ∊ D ; x₁ ≠ x₂ ⇒ f(x₁) ≠ f)x₂) Najprostszym przykładem f. różnowartościowej jest funkcja liniowa : f(x) = ax + b Inny przykład: f(x) = x³ Np funkcja kwadratowa f(x) = ax² +bx +c , nie jest różnowartościowa bo np. (−2) = (2)² = 4

5-latek: Moniko. ja wiem dzieci i inne sprawy ale teoria jest w ksiazce . Wiec zagladnij do niej i przeczytaj co to jest dziedzina i miejsce zerowe funkcji np . czy co to jest uklad rownan i kiedy jest sprzeczny ,oznaczony czy nieoznaczony . Co to jest nauka po nocach i kiedy jestes zmeczony po dniu to ja wiem ale to sa tak proste zadania ze .... nie dokoncze . Duzo teorii i zadan masz po lewej stronie (wystarczy kliknac

J: Dziedzina funkcji , to zbiór wszystkich argumentów x , dla których ta funkcja istnieje ( jest określona). Np f(x) = 3x + 5 ... dziedzina to zbiór liczb rzeczywistych D = R , bo za x możemy podstawić dowlną liczbę... , ale np jeżeli f(x) = √x , to dziedziną są tylko liczby nieujemne x ≥ 0 , bo nie istnieje ( w zbiorze liczb rzeczywistych) pierwiastek z liczby ujemnej.

	2x −5
Np. f(x) =		, dziedziną są wszystkie liczby rzeczywistwe oprócz x = 4 ,dla x = 4
	x −4

funkcja nie istnieje, bo mianownik byłby równy 0 ( 4 − 4 = 0) , a nie istnieje dzielenie przez zero

Monika: oj teoria tak znam uczyłam się i jest ok tylko ze jak przychodzi do przykładów to nie wiem co mam z nim zrobic dopiero jak ktos zacznie i ja zobacze a no to tak to dokoncze gubie sie.Jak bym mogła prosic o te przykłady podane nie teorie i zad 8 jak miałam to pytanie zdałam bezproblemu ale w zadaniu sie pogubilam

J: Z którym nie dajesz rady ?

Monika: to nie jest tak ze ja nie chce ja sie staram jedno wchodzi mi lepiej drugie gorzej chodzac zaocznie musze uczyc sie w domu zeby potrafic bo nie ma tam czasu na powtarzanie.

Monika: zad 6 7 8 a w ósmym podpunkt 1

Monika: przerazam sie jak widze piewiastek itp juz mysle ze sobie nie poradze choc wiem jaka jestteoria miesza mi sie to wszystko ..juz logarytmy nie sprawiały mi takich problemów. A jeszcze dzis chlopcy daja mi popalic

J:

	1
Zad 6) f(x) =		... napisałe Ci co to jest dziedzina .... tutaj mianownik
	(x −3)(x+2)

nie może być równy zero... kiedy iloczyn (x −3)(x +2) = 0 ?

Monika: nie ma poprostu kto przy mnie usiasc wytlumaczyc mi nawet podpowiedziec prócz w sumie tej strony zawsze ktos pomoze odpowie

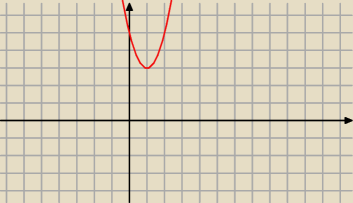
5-latek: W zadaniu nr 8 masz narysowac wykres funkcji y=2(x−1)²+3 Widziesz ze jest to postac kanoniczana funkcji wkwadratowej (postac y=a(x−p)+q Z niej mozeszsz odczytac wspolrzedne wierzcholka paraboli (masz je za darmo czyli mamy p=x_w=1 i q=y_w=3 (masz juz to do wykresu Zeby narysowc wykres musimy ta postac doprowadzic do postaci ogolnej czyli y=ax²+bx+c i z tej postaci oblicz miejsca zerowe tej funkcji czyli y=2(x−1)²+3 to y= 2(x²−2x+1)+3 wiemy ze (x−1)² to wzor skroconego mnozenia nwiec dalej to y= 2x²−4x+2+3 to y= 2x²−4x+5 teraz licz delte i miejsca zerowe czyli x₁ i x₂ i rysuj wykres (wi3emy ile jest miejsc zerowych w zaleznosci od delty ? tak ?

5-latek: Musisz wiedziec taka rzecz . jesli masz postac kanoniczna funkcji kwadratowej czyli y=a(x−p)+q to wspolrzedna p bierrzesz ze zmienionym znakiem do wykresu

5-latek: Ma byc oczywiscie y=a(x−p)²+q

5-latek: I jeszce jedna ciekawostka Jesli may wzor funkcji liniowej w postaci y=ax+b to wspolczynnik b informuje nas o tym w jakim punkcie wykres funkcji przetnie os OY Tak samo jest w przypadku funkcji kwadratowej Jesli mamy postac ogolna y=ax²+bx+c to wspolczynik c informuje nas o tym w jakim punkcie parabola przetnie os OY Masz tu taka postac y=2x²−4x+5 i zobacz na wykres z godsz 10:36