zadanie z geometrii wojtek: środkowa AD dzieli trójkąt ABC na dwa trójkąty, przy czym trójkąt ABD jest trójkątem równobocznym. Ile są równe pola trójkątów ADC i ABD, oraz jaką miarę ma kąt BAC

wojtek: ?

pigor: ..., np. tak :z warunków zadania : |AB|=|BD|=|AD|=CD| ⇒ |∡ADC|= 120^o i ΔADC równoramienny ⇒ |∡DCA|=|∡CAD|=30^o ⇒ |∡BAC|=90^o, natomiast pola trójkątów ADC i ABC są równe i tyle, gdybym miał podaną jakąś wielkość (długość) to może i bym ci policzył to pole . ...

wojtek: wie może jak policzyć to pole

wojtek: jaki wzór jest potrzebny

pigor: ..., nie mogę ci policzyć tego pola, bo czy na pewno wszystko co trzeba przepisałeś w treści zadania brakuje mi po prostu jakiejś danej wielkości liczbowej i... tyle .

wojtek: są jeszcze 2 wersje odpowiedzi'

	IADI2*√3
a) pole trójkąta ADC jest równe
	4

	{IABI}2*√3
b) pole trójkąta ABC jest równe
	2

wojtek: przepisałem zadanie poprawnie

wojtek: i nie wiem jak to rozwiązać

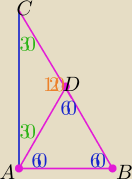
Eta: PΔrównobocznego o boku długości |AB|

	|AB|2√3
P(ABD)=
	4

Każda środkowa dzieli trojkąt na dwa trójkąty o równych polach to

	|AB|2√3
P(ΔADC)= P(ABD) zatem P(ABC)=2*		= ......
	4

pigor: ... nie wiem o co tu chodzi, bo z warunków zadania |AD|=|AB| i wg mnie pola o których mowa w zadaniu są równe, przy czym ΔABC − równoboczny o bokach AB=BD=AD, zaś ΔADC równoramienny, ale inaczej złożony z dwóch ekierek 30,60,90 przystających do tych w ΔABC... i tyle miałbym na ten temat ;

Eta:

pigor: ... no tak, ja piszę o ΔABC, a powinienem o ΔABD ; przepraszam ...

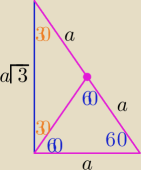
Eta: a=|AB|

	a2√3		|AB|2√3
P(ABD)=		=
	4		4

	1		a2√3		|AB|2√3
P(ABC)=		*a√3*a =		=
	2		2		2

i to wszystko