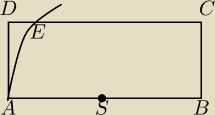
dowodzik majster: W prostokącie ABCD punkt S jest środkiem boku AB, |AB|>2|BC|. Poprowadzono łuk okręgu o środku w punkcie S i promieniu |AS|, który przeciął bok DC w punkcie E. Wykaż, że kwadrat o boku AD ma takie samo pole jak prostokąt, którego boki mają długość |DE| i |EC|.

pigor: ... ,z warunków zadania mam wykazać, że AD²= DE*DC, a widzę to np.z tw. stycznej DA i siecznej DC z punktu D poza okręgiem o środku w S, a F − drugi punkt przecięcia tego okręgu (łuku AE) z bokiem DC prostokąta to: DA²= DE*DF= DE*(DE+EF)= DE*DC i tyle ... c.n.w. ...