nierówność ania : nierówność IxI+IxI⁻¹≥sinIxI jest prawdziwa dla a) dla wszystkich x≠0 b) tylko dla x<0 c) tylko dla x>0 d) żadna z powyższych odpowiedzi nie jest prawdziwa o co chodzi w tym zadaniu?

wredulus_pospolitus: na pewno dla |x| > 1 (to na bank) dla x∊<−1;1> \ {0} także prawdziwe dla x=0 ... także

wredulus_pospolitus: polega to zadanie na zrozumieniu zbioru wartości funkcji sin x

ania : próbuje to rozwiązać i mi nie wychodzi pomógłby mi ktoś to zrobić

PW: Znana jest nierówność

	1
a +		≥ 2
	a

dla dodatnich a. Właśnie z tym mamy do czynienia.

ania : niestety nie mogę tego rozgryźć

J: Lewa strona nierówności jest zawsze ≥ 2 , a prawa jest zawarta w przedziale <−1,1 >, czyli .?

PW: Najpierw sprawdź, czy podana nierówność jest prawdziwa (można pomnożyć przez mianownik, bo jest dodatni i otrzymamy nierówność kwadratową). Nie ma co rozgryzać, w rozważanym zadaniu zamiast a napisali |x|: |x| + |x|⁻¹ to inna wersja

	1
a +		.
	a

ania : czyli odpowiedz d w takim razie ?

PW: A to myślisz, że jak coś jest zawsze większe od 2, to nie jest większe od sinusa?

magda: nie wiem właśnie ten przykład jest dla mnie nie zrozumiały

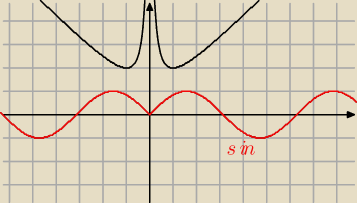
zawodus: Teraz widać?

J: A rozumiesz ... , że liczba 2 jest wieksza od liczby 1 ?

pigor: ..., weź sobie po lewej stronie dowolną liczbę ≥ 2 np 9, to masz nierówność 9 ≥ sin|x| , czyli prawde, czy fałsz dla x≠0 . ...

magda: prawda

magda: aniu to jest naprawde łatwe do zrozumienia