zaznacz na osi oxy zbiór rozwiązań
betty: polecenie jak w tytule, ale chodzi mi przede wszystkim o wyznaczanie dziedziny i zbioru
wartości funkcji.. jak się za to zabrać?
9x2−y2|y|−2 = 0
22 maj 15:23
J:
Dziedzina: IyI ≠ 2 ⇔ y ≠ 2 i y ≠ − 2
9x2 − y2 = 0 ⇔ y2 = 9x2 ⇔ √y2 = √9x2 ⇔ IyI = 3IxI
22 maj 15:36
betty: a to nie przeszkadza fakt, że zazwyczaj za dziedzinę bierze się x a za zbiór wartości y?
22 maj 15:40
PW: Jakąś "oś oxy" wymyśliłaś? Może po prostu "w układzie współrzędnych" − dziedzina i rozwiązania
są złożone z par (x,y) liczb rzeczywistych.
Jeżeli w mianowniku jest
|y|−2
(słabo widać), to musi być z dziedziny R×R wyrzucony zbiór par (x,y), dla których
|y|−2 = 0,
to znaczy dla których y=2 lub y=−2. Pary takie to dwie poziome proste:
k1={(x,y): x∊R∧y=2} oraz k2={(x,y): x∊R∧y=−2}. Dziedziną jest R×R\(k1∪k2). Rysujemy w
układzie współrzędnych dziedzinę (praktycznie − to co nie należy do dziedziny).
Rozwiązujemy równanie 9x2 − y2 = 0 i nanosimy na ten sam rysunek zbiór par (x,y)
spełniających to równanie. Odpowiedź − rozwiązaniami są te punkty (x,y), które spełniają
równanie 9x2 − y2 = 0 i należą do dziedziny
22 maj 15:42
PW: betty, co Ty opowiadasz/ Toż to funkcja
z dwóch zmiennych
| | 9x2 − y2 | |
z(x,y) = |
| . |
| | |y| − 2 | |
22 maj 15:44
J: Krótko mówiąc ... narysuj dwie proste : y = 3x oraz y = − 3x i " wyrzuć" z nich punkty o
rzędnych y =2 oraz y = −2
22 maj 15:45
J:
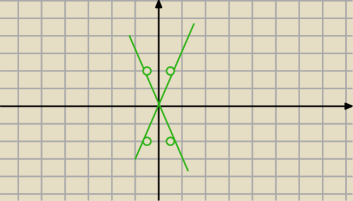
22 maj 15:48
J: Oczywiście "puste" kółka leżą na tych prostych...
22 maj 15:50
betty: oś oxy nie jest moim wymysłem wyobraźni, tylko moich wykładowców

ogarniam, dzięki.
22 maj 16:24
PW: Sala powinna buchnąć śmiechem i zażądać definicji

22 maj 16:53
zawodus: Nie zdziwiłbym się jakby "nadgorliwy" wykładowca jeszcze jakąś wymyślił

22 maj 16:55

 ogarniam, dzięki.
ogarniam, dzięki.

