Rozkład na czynniki
Radek: Jak rozłożyć na czynniki
4x3−7x+3 ?
Ma ktoś pomysł ?
21 maj 22:57
bezendu:
W(1)=0
W(x)=(x−1)(4x
2+4x−3)
| | 3 | | 1 | |
W(x)=(x−1)(x+ |
| )(x− |
| ) |
| | 2 | | 2 | |
21 maj 22:58
pigor: ..., w(1)=0, więc np. tak : 4x3−4x−3x+3= ... itd.
21 maj 22:59
Radek:
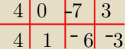
Podzieliłem przez 1 schematem Hornera i wyszło mi: 4x
2+x−6 i reszta − 3 gdzieś błąd popełniłem
?
21 maj 23:04
bezendu:
Wyżej masz już rozwiązanie. A po dwa zajrzy jak sie dzieli Hornerem bo od kiedy 1*4=1

?
21 maj 23:05
Eta:
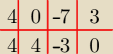
21 maj 23:08
Radek: Coś musiało mi się poknocić.
A czemu jeżeli w(1)=0 można to zapisać tak 4x3−4x−3x+3 ?
21 maj 23:10
bezendu:
Nie !
W(x)=(x−1)(4x2+4x−3)
21 maj 23:12
Radek: Mam na myśli to co napisał pigor
w(1)=0, więc np. tak : 4x3−4x−3x+3= ... itd.
21 maj 23:12
pigor: ... ano temu, bo wtedy ...

przewiduję sobie rozkład
np. tak :
4x3−7x+3= 4x
3−4x−3x+3= 4x(x
2−1)−3(x−1)= (x−1)[4x(x+1)−3]=
= (x−1)(4x
2+4x−3)= (x−1)[(2x)
2+2*2x*1+1−4]= (x−1)[(2x+1)
2−2
2]=
=
(x−1)(2x−1)(2x+3) .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
albo tak ...

:
4x3−7x+3= 4x
3−4x
2+4x
2−4x−3x+3= 4x
2(x−1)+4x(x−1)−3(x−1)=
= (x−1)(4x
2+4x−3)= i dalej możesz "swoja Δ−tą" , albo jak wyżej.

21 maj 23:26
Radek: Hmmy dzięki

To chyba trzeba mieć wyćwiczone by to zauważyć jak rozłożyć ?
21 maj 23:45
pigor: ... , no a co ty myślisz, że to tak z ...

nieba spada

to już Norwid (dawno o nim nic nie słyszałem) powiedział
pięknie, chyba coś tak :" ... Ty nad poziomy wylatuj ..."

22 maj 00:03
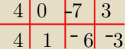 Podzieliłem przez 1 schematem Hornera i wyszło mi: 4x2+x−6 i reszta − 3 gdzieś błąd popełniłem
?
Podzieliłem przez 1 schematem Hornera i wyszło mi: 4x2+x−6 i reszta − 3 gdzieś błąd popełniłem
?
 ?
?
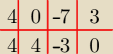
 przewiduję sobie rozkład
np. tak :
4x3−7x+3= 4x3−4x−3x+3= 4x(x2−1)−3(x−1)= (x−1)[4x(x+1)−3]=
= (x−1)(4x2+4x−3)= (x−1)[(2x)2+2*2x*1+1−4]= (x−1)[(2x+1)2−22]=
= (x−1)(2x−1)(2x+3) .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
albo tak ...
przewiduję sobie rozkład
np. tak :
4x3−7x+3= 4x3−4x−3x+3= 4x(x2−1)−3(x−1)= (x−1)[4x(x+1)−3]=
= (x−1)(4x2+4x−3)= (x−1)[(2x)2+2*2x*1+1−4]= (x−1)[(2x+1)2−22]=
= (x−1)(2x−1)(2x+3) .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
albo tak ... :
4x3−7x+3= 4x3−4x2+4x2−4x−3x+3= 4x2(x−1)+4x(x−1)−3(x−1)=
= (x−1)(4x2+4x−3)= i dalej możesz "swoja Δ−tą" , albo jak wyżej.
:
4x3−7x+3= 4x3−4x2+4x2−4x−3x+3= 4x2(x−1)+4x(x−1)−3(x−1)=
= (x−1)(4x2+4x−3)= i dalej możesz "swoja Δ−tą" , albo jak wyżej. 
 To chyba trzeba mieć wyćwiczone by to zauważyć jak rozłożyć ?
To chyba trzeba mieć wyćwiczone by to zauważyć jak rozłożyć ?
 nieba spada
nieba spada  to już Norwid (dawno o nim nic nie słyszałem) powiedział
pięknie, chyba coś tak :" ... Ty nad poziomy wylatuj ..."
to już Norwid (dawno o nim nic nie słyszałem) powiedział
pięknie, chyba coś tak :" ... Ty nad poziomy wylatuj ..." 