Geometria analityczna
Marcin: 1) Napisz równanie okręgu oʹ, będącego obrazem okręgu o opisanego równaniem x2 + y2 − 4y − 5 =
0 w symetrii względem początku układu współrzędnych.
2) Napisz równanie okręgu opisanego na kwadracie ABCD, którego przeciwległymi
wierzchołkami są punkty A = (1, −3) i C = (3, 5).
3) Wykaż, że okręgi o równaniach (x −1)kwadrat + (y − 3)kwadrat = 1,6 , i (x + 2)kwadrat + (y −
2)kwadrat = 3,6 , są styczne zewnętrznie.
4) Punkty A = (−2, −4) i C = (4, 8) są przeciwległymi wierzchołkami rombu ABCD. Długość
jego przekątnej BD jest równa 4{5} . Wyznacz współrzędne wierzchołków B i D tego rombu.
Byłaby możliwość rozwiązania z wytłumaczeniem? Nie najlepiej mi idzie z tego działu pomocy

21 maj 18:13
Marcin: w czwartym jest 4 pod pierwiastkiem z 5

21 maj 18:14
Marcin: ktokolwiek, cokolwiek

?
21 maj 19:15
Marcin:
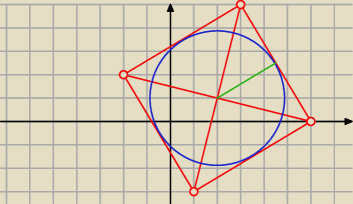
2)
21 maj 19:19
Marcin: Okrąg ma być opisany, przepraszam. (Ale wiadomo o co chodzi)

21 maj 19:21
Janek191:
z.1
x2 + y2 − 4y − 5 = 0
( x − 0)2 + ( y − 2)2 − 4 − 5 = 0
( x − 0)2 + ( y − 2)2 = 32
S = ( 0; 2) r = 3
Znajdujemy S' = ( x' ; y' )
x' = − x = 0
y' = − y = − 2
r' = r = 3
więc
Odp. ( x − 0)2 + ( y + 2)2 = 9
========================
21 maj 20:02
Janek191:
z.3
( x − 1)
2 + ( y − 3)
2 = 1,6
więc
S
1 = ( 1; 3) oraz r
1 =
√1,6
( x + 2)
2 + ( y − 2)
2 = 3,6
więc
S
2 = ( − 2; 2) oraz r
2 =
√3,6
zatem I S
1 S
2 I
2 = ( − 2 − 1)
2 + ( 2 − 3)
2 = 9 + 1 = 10
czyli I S
1 S
2 I =
√10
| | 4 | | 6 | |
r1 + r2 = √1,6 + √3,6 = √1610 + √3610 = |
| + |
| = |
| | √10 | | √10 | |
Mamy I S
1 S
2 I = r
1 + r
2 , więc dane okręgi są styczne zewnętrznie.
21 maj 20:17
Marcin: Janek wielkie dzięki za pomoc, Marcin mógłbys do tego obliczenia zrobić? To co mi narysowałeś
sam również narysowałem, albo, który wzór zastosować

? Tak wiem, jestem bardzo w plecy
21 maj 20:40
Janek191:
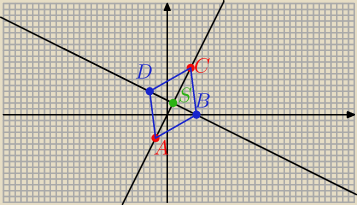
z.4
I B D I = 4
√5
A = ( − 2; − 4) C = ( 4; 8)
S − środek odcinka AC
| | − 2 + 4 | | − 4 + 8 | |
xs = |
| = 1 ys = |
| = 2 |
| | 2 | | 2 | |
S = ( 1; 2)
Równanie prostej AC :
y = a x + b
− 4 = − 2a + b
8 = 4a + b
−−−−−−−−−−−−− odejmujemy stronami
8 − (−4) = ( 4a + b ) − ( − 2a + b)
12 = 6a
a = 2
−−−−−
b = 8 − 4a = 8 − 4*2 = 0
−−−−−−−−−−−−−
y = 2 x
======
Prosta BD jest prostopadła do pr AC i przechodzi przez S = ( 1; 2)
2*a
2 = − 1 ⇒ a
2 = −
12
y = − 0,5 x + b
2
2 = −0,5*1 + b
2
b
2 = 2,5
y = − 0,5 x + 2,5
============
Punkty B i D leżą na tej prostej, więc
B = ( x; y) = ( x; −0,5 x + 2,5)
oraz
I BS I = I D S I = 0,5*4
√5 = 2
√5 ⇒ I BS I
2 = 4*5 = 20
( 1 − x)
2 + ( 2 − ( −0,5 x + 2,5))
2 = 20
1 − 2x + x
2 + ( 0,5 x − 0,5 )
2 = 20
1 − 2x + x
2 + 0,25 x
2 − 0,5 x + 0,25 = 20 / * 4
4 − 8 x + 4x
2 + x
2 − 2x + 1 = 80
5 x
2 − 10 x − 75 = 0 / : 5
x
2 − 2x − 15 = 0
Δ = 4 − 4*1*(−15) = 64
√Δ = 8
| | 2 − 8 | | 2 + 8 | |
x = |
| = − 3 lub x = |
| = 5 |
| | 2 | | 2 | |
zatem
y = −0,5*(−3) + 2,5 = 4 lub y = − 0,5*5 + 2,5 = 0
zatem
B = ( 5; 0) i D = ( − 3; 4)
=====================
21 maj 20:56
Janek191:
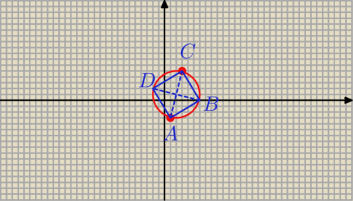
z.2
A = ( 1; − 3) C = ( 3; 5)
S − środek kwadratu i równocześnie środek okręgu opisanego na kwadracie
| | 1 + 3 | | − 3 + 5 | |
xs = |
| = 2 ys = |
| = 1 |
| | 2 | | 2 | |
S = ( 2; 1)
r
2 = I AS I
2 = ( 2 − 1)
2 + ( 1 − (−3))
2 = 1 + 16 = 17
Równanie okręgu
( x − x
s)
2 + ( y − y
s)
2 = r
2
czyli
( x − 2)
2 + ( y − 1)
2 = 17
=====================
21 maj 21:08
Marcin: Dzięki Janek za pomoc w tym wieczorze, wszystkie zadania zrozumiane, jedynie co sprawia
ostatnie problemy, ale wszystko z czasem, dzięki jeszcze raz
21 maj 21:58
Marcin: Marcin wybacz że nie dokończyłem obliczeń, ale nie widziałem tego wpisu. Na szczęście Janek dał
radę

21 maj 22:16


 ?
?
 2)
2)

 ? Tak wiem, jestem bardzo w plecy
? Tak wiem, jestem bardzo w plecy
 z.4
I B D I = 4 √5
A = ( − 2; − 4) C = ( 4; 8)
S − środek odcinka AC
z.4
I B D I = 4 √5
A = ( − 2; − 4) C = ( 4; 8)
S − środek odcinka AC
 z.2
A = ( 1; − 3) C = ( 3; 5)
S − środek kwadratu i równocześnie środek okręgu opisanego na kwadracie
z.2
A = ( 1; − 3) C = ( 3; 5)
S − środek kwadratu i równocześnie środek okręgu opisanego na kwadracie
