Oblicz pole trójkąta Sandra: Oblicz pole trójkąta a,b,c, w którym: c)ab=√3 ,bc=√2 ,ac=2

Utem: c=√3 b=2 a=√2 Z tw. cosinusów: a²=b²+c²−2ac cosα √2²=2²+√3²−2*2*√3 cosα 2=4+3−4√3 cosα

	5
cosα=
	4√3

sin²α+cos²α=1

	25
sin2α=1−
	48

	23
sin2α=
	48

	√23
sinα=
	√48

	1		√23		√23
PΔ=		*2*√3*sinα=√3*		=
	2		√48		√16

	√23
pΔ=
	4

Janek191: @Utem Popatrz na tw. cosinusów a² = b² + c² − 2b*c*cos α

Utem: Dziękuję, literówka. Dobrze podstawiłam. Sprawdzałes może moje rachunki?

Janek191: Jest ok

Utem: Pozdrawiam.

Sandra: ja znalazłam wzór c2=a2+b2−2abcosα, więc są już trzy wersje.... z którego korzystać? jeśli mój jest poprawny to sinα=^√7_√32 ale nie wiem co dalej

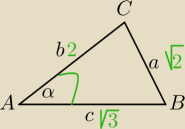
5-latek: To popatrz na rysunek Utem i przeczytaj jeszce raz twierdzenie cosinusow Wtedy bedziesz wiedziec ktory wzor zastosowac

Utem: Witaj 5−latek. Popatrz Sandra , jak poprawił Janek mój wzór . Jeśli chcesz obliczyć cos α, to wzór: a²=b²+c²−2b*c cosα Musisz wiedzieć po co stosujesz tw. cosinusów.