trygonometria
Subaru: Rozwiąż równanie:
Tak to robię
| | √3 | | π | | 5π | |
− |
| =cos(π− |
| )=−cos |
| |
| | 2 | | 6 | | 6 | |
czyli
| | 5π | | 2 | | 5π | | 2 | |
x= |
| + |
| kπ lub x=− |
| + |
| kπ |
| | 18 | | 3 | | 18 | | 3 | |
więc
| | 17π | | 7π | | 5π | | 5π | | 7π | | 17π | |
x∊{− |
| , − |
| , − |
| , |
| , |
| , |
| } |
| | 18 | | 18 | | 18 | | 18 | | 18 | | 18 | |
Proszę bardzo o sprawdzenie.
21 maj 17:23
Subaru: HELP
21 maj 17:41
Subaru: HELP
21 maj 17:54
Mila:
Sprawwdzam.
21 maj 18:04
Mila:
Zgadza się.
Trochę inaczej ustalam serię rozwiązań.
21 maj 18:13
Subaru: Mianowicie?

21 maj 18:14
Mila:
Może nie będę Ci mącić w głowie. Wyniki są dobre. Każdy nauczyciel trochę inaczej uczy.
21 maj 18:16
Subaru: Ok. W takim razie dzięki

21 maj 18:18
Mila: 
21 maj 18:21
Subaru: A to?

4sin
4−5cos
2x−1=0
| | 2 | |
Wiem, że trzeba równanie kwadratowe, ale mi tam wychodzi sin2= |
| i nie wiem co z tym |
| | 3 | |
zrobić.
21 maj 18:37
jakubs: | | √2 | | √2 | |
czyli sinx= |
| lub sinx=− |
| |
| | √3 | | √3 | |
I usunąć niewymierność z mianownika.
21 maj 18:40
razor: 4sin
4x − 5cos
2x − 1 = 0
4sin
4x − 5(1−sin
2x) − 1 = 0
4sin
4x + 5sin
2x − 6 = 0
Δ = 25 + 4*4*6 = 11
2
| | −5−11 | | −5+11 | | 3 | |
sin2x = |
| < 0 lub sin2x = |
| = |
| |
| | 8 | | 8 | | 4 | |
dalej chyba wiesz?
21 maj 18:43
Subaru: | | √6 | |
Ale nie wiem ile wynosi sinx= |
| (?) |
| | 3 | |
21 maj 18:43
Lukas:
4sin
4(x)−5cos
2(x)−1=0
4sin
4(x)−5(1−sin
2(x))−1=0
4sin
4(x)−5+5sin
2(x)−1=0
4sin
4(x)+5sin
2(x)−6=0
sin
2(x)=t t∊<−1,1>
4t
2+5t
2−6=0
Δ
t=121
√Δt=11
t
1=−2 ∉<−1.1>
| | √3 | | √3 | |
sin(x)= |
| lub sin(x)=− |
| |
| | 2 | | 2 | |
21 maj 18:44
Subaru: Dobra, teraz już wiem gdzie miałem błąd. Dzięki!
21 maj 18:45
razor: wskazówka: jak masz coś takiego jak wyżej to żeby skrócić liczbę rozwiązań można zamienić
sin
2x na cos2x w taki sposób
cos2x = 1 − 2sin
2x
21 maj 18:45
jakubs: 4sin
4x−5(1−sin
2x)−1=0
4sin
4x+5sin
2x−5−1=0 sin
2x=t ; t∊(0,1>
4t
2+5t−6=0
Δ=25+24=49
√Δ=7
21 maj 18:45
Mila:
To masz błąd.
Napisz to poprawię.
21 maj 18:45
Lukas:
jakubs źle !
21 maj 18:46
Subaru: Rozwiązań do wyboru, do koloru

21 maj 18:47
jakubs: U mnie źle, ja odpadam z zadankami dzisiaj. Wybaczcie

21 maj 18:47
jakubs: Lukas jeżeli sin2x=t to t∊<0,1>
21 maj 18:49
Lukas:
Moja rozwiązanie jest poprawne.Wystarczy, że dokończysz wypisując z tabelki i korzystając z
wykresu sin(x).
21 maj 18:49
Subaru: A jeśli chodzi o to:
| 1 | |
| x2 przeniosłem na prawą. Wychodzi kwadratowe, które jest zawsze ujemne. Co teraz trzeba |
| 2 | |
zrobić?
21 maj 19:28
Subaru: Jeszcze to
cos2x + 4cosxsinx + 3sin2x=0
Ktoś? Coś?
21 maj 20:03
Utem:
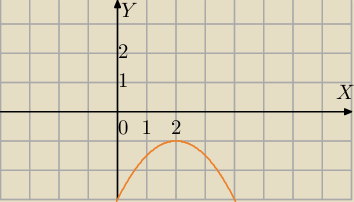
x≠0
| | 1 | |
Badamy zbiór wartości f(x)=− |
| x2+2x−3 |
| | 2 | |
| | 1 | |
f(2)=− |
| *22+2*2−3=−1 największa wartość f(x) |
| | 2 | |
Stąd tylko
x=2 może być rozwiązaniem tego równania
spr.
odp.
x=2
21 maj 20:04
Subaru: Dzięki

To jeszcze tylko jedno
cos
2x + 4cosxsinx + 3sin
2x=0
21 maj 20:15
Utem:
Rozwiąż równanie
cos2x + 4cosxsinx + 3sin2x=0⇔
cos2x−sin2x+4cosx sinx +4sin2x=0
(cosx−sinx)*(cosx+sinx)+4sinx*(cosx+sinx)=0
(cosx+sinx)*(cosx−sinx+4sinx)=0
cosx+sinx=0 lub cosx+3sinx=0⇔
sinx=−cosx lub 3sinx=−cosx
dokończysz?
21 maj 20:34
razor: można też tak:
3sin
2x + 4sinxcosx + cos
2x = 0 − Zauważam, że cosx = 0 nie jest rozwiązaniem tego równania
(dlaczego?) i dzielę równanie obustronnie przez cos
2x
| 3sin2x | | 4sinxcosx | |
| + |
| + 1 = 0 |
| cos2x | | cos2x | |
3tg
2x + 4tgx + 1 = 0
Δ = 16−12 = 2
2
| | −4−2 | | 1 | |
tgx = |
| = −1 lub tgx = − |
| |
| | 6 | | 3 | |
22 maj 10:49
Subaru: Dzięki. Pomożecie w tym: ?
Chodzi mi przede wszystkim o to jak to zacząć

22 maj 19:52
Subaru: | | 1 | |
Podniosłem do kwadratu i wyszło sin2x= |
| Jaka powinna być odpowiedź? Bo mam pewną |
| | 2 | |
niezgodność z odpowiedzią z książki.
22 maj 20:04
Subaru: SOS
22 maj 20:09
Mila:
| | 1 | |
sinx *cos45o−sin45*cosx= |
| |
| | 2 | |
| | π | | π | | π | | 5 | |
x− |
| = |
| +2kπ lub x− |
| = |
| π+2kπ |
| | 4 | | 6 | | 4 | | 6 | |
| | 5 | | 13 | |
x= |
| π+2kπ lub x= |
| π+2kπ |
| | 12 | | 12 | |
===========================
22 maj 21:38



 4sin4−5cos2x−1=0
4sin4−5cos2x−1=0



 To jeszcze tylko jedno
cos2x + 4cosxsinx + 3sin2x=0
To jeszcze tylko jedno
cos2x + 4cosxsinx + 3sin2x=0
