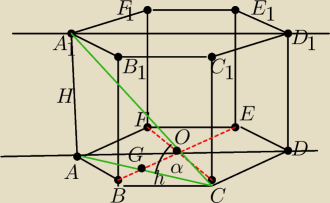
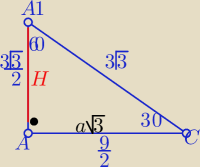
Aguś:): Potrzebuje te zadanko..inne zrobilam, ale to mi nie wychodzi:(..Krotsza przekatna graniastosłupa prawidlowego szesciokatnego ma dlugosc 3√3 i jest nachylona do plaszczyzny podstawy pod katem 30stopni. Oblicz objetosc i pole powierzchni całkowitej tego graniastoslupa.

M:

Mei Lin: |A₁C|=3√3− krótsza przekątna graniastosłupa |∡ACA₁|=α=30^o kąt nachylenia krótszej przekątnej do płaszczyzny podstawy |AA₁|=H =? wysokośc graniastosłupa |AG|=|GC|=h wysokośc trójkata równobocznego w podstawie graniastosłupa |AC|=2h W trójkącie prostokatnym ACA₁ o kątach 30^o,60^o 90^o |A₁C|=3√3 więc

	3√3
|AA1|=H=
	2

	3√3*√3		9
|AC|=2h=		=
	2		2

	9
Stąd ||GC|=h=
	4

W trójkącie równobocznym BCO

	a√3
h=
	2

a√3		9
	=
2		4

4a√3=18

	18		18√3		3√3
a=		=		=
	4√3		12		2

	3√3
Bok szesciokata w podstawie ma długośc a=
	2

Pole podstawy P_p

	3a2√3
Pp=
	2

	27		1
Pp=3*		√3*
	4		2

	81
Pp=		√3
	8

V=P_P*h

	81		3√3		729
V=		√3*		=		jm3
	8		4		32

Pole całkowite P_c P_c=2P_p+P_b P_c=2P_p+6*a*H

	81√3		3√3		3√3
Pc= 2*		+6*		*
	8		2		2

	81√3		27
Pc=		+6*
	4		4

	81√3		81√3+162
Pc=		+162}{4}=		=
	4		4

	81(√3+2
=		jm2
	4

	729
Odp. Objętośc graniastosłupa wynosi V=		jm3 a pole powierzchni całkowitej wynosi
	32

	81(√3+2
Pc=		jm2
	4

Prosze sprawdzić

Mała LI:

	9		3√3
2hp=a√3=		⇒ a=		=H ( ściany boczne są kwadratami)
	2		2

	27		81√3
a2=		i a3=
	4		8

	3a2√3		81√3
Pp=		=
	2		8

	3a3√3		9*81
V=Pp*a=		=
	2		16

	729
V=
	32

========= P_c=2P_p+6a²

	81√3		162
Pc=		+
	4		4

	81(√3+2)
Pc=
	4

==============

Mei Lin: Dziękuję bardzo