wartość parametru m i Zbior wartości Czarek: Witam potrzebuje pomocy w 2przykladac 1) dla jakich wart. parametru m równanie f(x)=m ma rozwiązanie w przedziale <−1,2> f(x)= x⁵−5x+4

	x2−x+1
2) Wyznacz zbiór wartości funkcji f(x)=		w przedziale <0,2>
	x2+x+1

Czarek: up!

Mila: Studia czy LO?

razor: Jaki poziom?

razor: o Mila mnie ubiegła

Czarek: LO

Czarek: up!

Hugo: hahahah ;3 − potrzebuje zadanko wychodzi z delty że mi x=−√1 co teraz? − Lo czy studia? − Lo − a to wpisz że sie nie da

Hugo: Czarek: policz dla skrajnych przedziałów −1 oraz 2 podstawiając za 'x' oraz Horner proponuje i pierwiastki poszukać ewentualnie wierzchołek ale to gdybanie. x⁵−5x+4=m

Mila: Czarek trzeba zbadac przebieg wykresu funkcji. Do tego potrzebna umiejętność liczenia pochodnych, a przeciez nie masz tego w LO, więc z jakiego zbioru to zadanie?

Czarek: tez tak robiłem wyszlo mi m=8 i m=26. Później też pochodną zrobiłem tej funkcji i wyszły mi 3iksy x=0 x=1 x=−1. Zrobiłem wykres i nie wiem co dalej W odpowiedziach jest przedziam m należy(0;26>

Czarek: Mila, Reforma była naszego Ministerstwa, i jestem pierwszym rocznikiem które analize ma w progrmie LO jest to zadanie z podrecznika wydawnictwa Nowej Ery "Matematyka 2"

Mila: Czarek, Napisz jaką wiedzą dysponujesz do badania funkcji, od tego zależy sposób, który zrozumiez. Hugo nie rozumiem Twojego problemu: ( Może napisz w innym wątku zadanie) √1=1 √−1=i

Mila: Piszę, wiem, umiesz liczyc pochodne i ekstrema.

Czarek: Umiem liczyc: −pochodną funkcji −Granice −Najmniejsza i Najwięksa wartosc funkcji −monotonicznosc, ekstremum

Hugo: ... Milo to był kawał matematyczny. Wiem wiem czytałem o zespolonych w konsekwencji wczorajszego poradnictwa na forum gdzie mówiłaś by sie nie uczyc o zespolonych tylko nadrobić braki

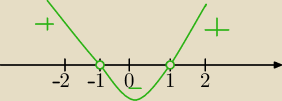
Mila: f(x)=x⁵−5x+4 f'(x)=5x⁴−5 f'(x)=0⇔5x⁴−5=0 ⇔x=1 lub x=−1 to kandydaci na ekstrema f'(x)>0⇔f(x) jest rosnąca x⁴−1>0⇔(x²+1)*(x²−1)>0⇔ (x−1)*(x+1)>0⇔ Patrz teraz na oś W punktach −1 i 1 pochodna zmienia znak⇔że tam są ekstrema Patrząc od lewej f(x) rosnąca dla x∊(−∞,−1) dla x∊<−1, 1) funkcja f(x) jest malejąca⇔ dla x=−1 jest maksimum y_maks=−1+5+4=8 Dalej Dla x>1 funkcja jest cały czas rosnąca w x=1 jest min y_min=0 Teraz zbadamy wartość na końcu przedziału f(2)=2⁵−5*2+4=22+4=26⇔ Najmniejsza wartość funkcji w przedziale <−1,2> wynosi 0 Największa wartość funkcji w przedziale <−1,2> wynosi 26⇒ Równanie : x⁵−5x+4=m ma rozwiązanie dla m∊<0,26> Podać inny sposób?

Lukas: To nie jest zadania na starą maturę ?

Mila: Hugo nie mówiłam, że masz się nie uczyć o zespolonych. To akurat wdzięczny dział i rozwiązuj zadanka.

Mila: Lukas to nowa matura, która będzie w przyszłym roku. Czarek naszkicuj sobie wykres.

Czarek: Mila, Dzięki wszystko już jest zrozumiane Pozdrawiam.

Mila: Świetnie. No to drugie teraz? Czy ma być zbiór wartości tylko w przedziale?

Czarek: tak

Hugo: Milo zostań rektorem na uczelni

Mila: W takim razie jaką masz koncepcję? Zauważ, że f(x) przyjmuje tylko wartości dodatnie.

Czarek: Podstawiłem za iksa wartości końca przedziału 0 i 2. Później policzylem pochodna ale nic z tego nie wyszlo i dalej nie wiem co /

Lukas: Ale ja i tak jeszcze będę pisał starą bo mam 5 lat na to

Czarek: wyszło źle policzylem pochodna na początku ale pozniej wyszlo ładnie. Ekstrem max x=−1 −−−> y=3 nie należy do przedziału Ekstrem min x=1−−−> y=1/3 f(−2)=7/3 f(0)=1 Czyli bedzie przedział <1/3;1> tak

Czarek: Lukas to te tematy chyba nie wchodzą w zakres Twojej matury

Mila: Dlaczego liczysz wartość dla (−2) ? Masz podany przedział <0,2>

Czarek: pomyłka będzie oczywiscie f(2)=3/7

Mila: Tak.