Jednym z miejsc zerowych funkcji f(x) = ax^2 - 2x - 21 jest 3. Znajdź drugie mie arianne: Jednym z miejsc zerowych funkcji f(x) = ax² − 2x − 21 jest 3. Znajdź drugie miejsce zerowe funkcji f.

ICSP: f(3) = 0

J: Jak napisał "ICSP" ... i oblicz a.

arianne: f(3) = 0 3 = 9a − 6 − 21 3 = 9a − 27 9a = −30 a = ⁻¹⁰ ₃ i potem to a wstawiam w podany wzór funkcji i obliczam miejsce zerowe?

ICSP: źle wstawione.

Nieuchwytny: Liczysz f(3)=0 f(3)=9a²−6−21

Nieuchwytny: Oczywiście ma być 9a−6−21=0

J: Odwrotnie podstawiłaś ..za x podstawiasz 3

J:

	b
Masz a = 3 i oraz x1 = 3 i teraz : x1 + x2 = −
	a

arianne: 3 + x₂ = ²₃ / −3 Czy o to chodzi? Przyznam, że nie pamiętam bym miała do czynienia z podobnym zadaniem, wolę się więc upewnić.

arianne: ?

kejt: wzory Viet'ea

Kaska: obliczone juz sa a=3 b=−2 c=−21. Liczysz Δ=b² − 4ac Δ= 256 √Δ=16 x₂= −b+√Δ pod kreską ułamk. 2a x₂= 3

Ktosiek: Czy ktoś mógłby mi wytłumaczyć jak dokładnie to zrobić? Bo widzę tu wiele wersji i jaka jest poprawna

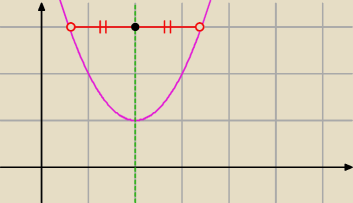
chichi: bo rozwiązań jest więcej niż jedno z warunku w poleceniu wynika, że f(3) = 0 ⇔ a*3² − 2*3 − 21 = 0 ⇔ a = 3. czyli mamy, że f(x) = 3x² − 2x − 21 i teraz można np. tak: (1) wzorami... czyli liczymy Δ = ..., a więc x₁ = ... lub x₂ = ... (jedno z nich to 3) (2) z własności f. kwadratowej mianowicie, że posiada ona oś symetrii (patrz rysunek)

	x1 + x2		b
p =		, a z drugiej strony masz wzór z postaci ogólnej p = −		.
	2		2a

Jolanta: Wiesz co to jest miejsce zerowe?

Jolanta: Jeżeli parabola przecina os x to mamy 2 miejsca zerowe i wtedy Δ>0 Miejsce zerowe to taki x dla którego y=0 f(x)=ax²−2x−21. albo y=ax²−2x−21 f(3)=0 0=a*3²−2*3−21 0=9a−27 a=3 f(x)=3x²−2x−21 Teraz mozemy policzyć Δ i pierwiastki czyli miejsca zerowe Albo możemy policzyć wierzchołek paraboli i drugie miejsce zerowe 1) Δ=b²−4ac=(−2)²−4*3*(−21)=4+252=256

	−b+√Δ		2+16
x1=		=		=3. to miejsce zerowe już znamy
	2a		2*3

	−b−√Δ		2−16		−14		−7		1
x2=		=		=		=		=−2
	2a		2*3		6		3		3

A teraz drugi sposób liczymy współrzędna x wierzcholka

	−b		2		1
xw=p=		=		=
	2a		2*3		3

I drugi wzór na x_w

	x1+x2
xw=
	2

1		3+x2
	=		\*2
3		2

2
	=3+x2
3

	1
−2		=x2
	3