Wykres funkcji Tomasz:

	6
Witam. Mam narysować układ współrzędnych i umieścić na nim wykresy funkcji f(x) =		dla
	x+1

x (−∞,−1)(−1,∞) oraz g(x)= 6x+6 dla x R. Następnie korzystając z rysunku muszę podać współrzędne punktów wspólnych. Totalnie mi to nie wychodzi. Tzn. Podstawiam dla f(x) (funkcja wymierna) −2,−3−4, dla g(x) (funkcja liniowa) −2 i 0. Rysuję to w układzie współrzędnych i nie widzę żadnych punktów wspólnych obu wykresów. Może mi ktoś wyjaśnić jak wykonać to zadanie ?

J:

	6
Narysuj f(x) =		i przesuń wzdłuż osi OX o jeden w lewo ... potem g(x) = 6x + 6
	x

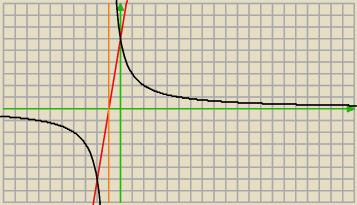
5-latek: widziosz punkty wspolne tych wykresow ?

Tomasz: tak właśnie robię. f(x) dla x=−4 y= −1,5, dla x=−3, y=−2, dla x=−2, y=−3. Przesuwam to o [−1,0] (czyli po prostu x=−5, x=−4, x=−3). Następnie rysuję g(x) dla x=−2, y=−6, Dla x=0, y=6. Nie widzę tutaj żadnych punktów wspólnych.

5-latek: To jakie TY nosisz okulary +30? Nie widzisz punktow przeciecia sie wykesu czarnego i czerwonego ? Masz dwa punkty

Tomasz: @5−latek: [−1,−6] i [1,7] patrząc na układ przesunięty o 1 w lewo.

Tomasz: gdy pisałem wcześniejszy post nie było jeszcze twojego wykresu.

5-latek: Tak jak CI napisal J wyzej

5-latek: Wiadomo dlaczego dziedzina f(x) jest zbior R\{−1}? tak ?

Tomasz:

	6
Tak, ponieważ w mianowniku nie możemy mieć 0. Gdybyśmy podstawili x=−1 wówczas		nie
	−1+1

miało by sensu. btw. Punkty wspólne odczytuję tylko w obrębie wykresu (tzn. tylko punkty które przechodzą przez f(x) dla x= −4,−3,−2,−1/2,−1/3,−1/4,1/4,1/3,1/2,2,3,4 i przez g(x) dla x= −2, 0) czy poza wykresem również ? Mam na myśli to, że rysując hiperbolę przez cały wykres (będzie się zbliżała do x i y, ale nigdy ich nie przetnie) oraz ciągnąć linie funkcji liniowej przechodzącej przez te punkty[−2,−6] i [0,6] pewne jest, że kiedyś w końcu się przetną.

5-latek: raczej (0,6) i (−2,6)

5-latek: Dobrze napisale (−2,−6)

Tomasz: g(x) = 6x+6 dla x=−2 6*(−2)+6 = −12+6 = −6 dla x =0 6*0+6 = 6

5-latek: To nie tak Tomku Aby wyznaczyc punkty przeciecia sie wykresow musisz przyrownac te dwie funkcje do siebie czyli

	6
		=6x+6 z tego wyznaczysz x −sy i potem wyliczone xy wstawiasz do rownania funkcji
	x+1

g(x) i liczysz y _ki. tak wyznaczasz algebraicznie

Tomasz: Taki sposób na punkty przecięcia znam, jednakże polecenie mówi, aby wszystko zrobić graficznie.

	6
Tzn. Na 1 układzie współrzędnych narysować wykres f(x)=		i g(x)= 6x+6 i korzystając z
	x+1

tego rysunku podać współrzędne punktów wspólnych obu wykresów oraz dla jakich argumentów wartości funkcji F są nie mniejsze niż wartości funkcji g(x). Gdybym miał to robić korzystając ze wzorów to dawno bym przyrównał do siebie oba. Chodzi tutaj o odczytanie wszystkiego z rysunku.

J: ⇔ 6 =(6x+6)(x+1) ⇔ 6x² + 6x +6x + 6 = 6 ⇔x² + x = 0 ⇔ x(x+2) = 0 ⇔ x =0 lub x = −2 g(0) = f(0) = 6 , g(−2) = f(−2) = − 6 , A(0,6) B(−2,−6)

J: To kup sobie papier milimetrowy ( jeśli jeszcze taki istnieje), najlepiej formatu A0 , zaostrz dobrze twardy ołówek (najlepiej H6) i rysuj , przyjmując jednostkę na osiach 1 mm.

5-latek: J Nie wiem czy az tak duze ale bloki milimetrowe sa w sprzedazy

Tomasz: J − ale po co te nieuprzejmości... Tak po prostu brzmi polecenie.

	6
Dokładnie: "Narysuj w jednym układzie współrzędnych wykresy funkcji f(x)=		dla x
	x+1

(−∞,−1)(−1,∞) i g(x)=6x+6 dla x R. a) Skorzystaj z rysunku i podaj współrzędne punktów wspólnych obu wykresów b)odczytaj dla jakich argumentów wartości funkcji f są nie mniejsze niż wartości funkcji g(x)."

J: To poskleja te A4.....jaki problem ? ..

J: Poleceni tak brzmi .... żebyś naszkicował wykres, jako ilustrację rozwiązania

Tomasz: tzn. że mam nie korzystać z tabelek itd. A jedynie wszystko wyliczyć ze wzorów i dopiero na końcu narysować układ współrzędnych z hiperbolami przechodzącymi przez A(0,6) B(−2,−6) oraz z prostą przechodzącą przez A(0,6) B(−2,−6) ? i od razu a propos b) f(x)≥g(x)

6
	≥ 6x+6
x+1

6 ≥ (6x+6)(x+1) 6 ≥ 6x² + 6x +6x + 6 0 ≥ x² + 2x 0 ≥ x(x+2) Zamieniam na nierówność x(x+2) = 0 x₁ = 0 x₂ = −2 Zatem f(x) ma wartości nie mniejsze od g(x) gdy x∊(−2,0) ?

Tomasz: odświeżam

J: Tak.