geometria analityczna Martyna : Napisz równanie okręgu który jest obrazem okręgu o środku S=(3;−2) i promieniu 8 w symetrii względem prostej y=x+4

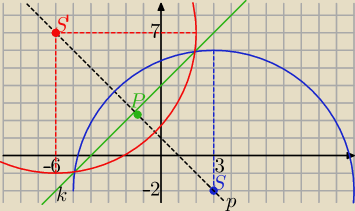
Eta: Szukamy punktu S^'(x_S^',y_S^') prosta k: y=x+4 prosta p⊥k i przechodząca przez S ma równanie: p: y=−(x−3)+2 ⇒ y=−x+1 rozwiązując układ równań tych prostych wyznaczamy punkt P, który jest środkiem odcinka SS^' { y=x+4 {y= −x+1 ⇒ x=−1,5 i y=2,5 to x_S^'=2x_P−x_S ⇒ x_S^'=−6 y_S^'=2y_P−y_S ⇒ y_S^'=7 S^'(−6,7) i r=8 o^' : (x+6)²+(y−7)²=64