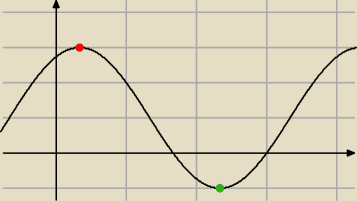
tryg ciekawsky: Bazując na diagramie znajdz wspolczynniki a,b,c,d funkcji f(x)= a*sin(bx+c)+d czerwony punkt = (1/3,3) zielony punkt = (7/3, −1) a=(3−(−1))/2=2 d=(3+(−1))/2=1 okres = (7/3−1/3)*2=4 4=2π/b → b=π/2 i tu moja bolączka − czy jest jakiś łatwiejszy sposób na wyliczenie c niż: y=2sin(π/2x+c)+1 3=2sin(π/2*(1/3)+c)+1 sin(π/6+c)=1 sin(π/6+c)=sin(π/2) π/6+c=π/2+2kπ c=π/3+2kπ

	π		π
y=2sin(		x+		)+1
	2		3

(?)

ZKS: Nie wiem czy łatwiejszy to sposób. Jeżeli otrzymałeś funkcję

	π
y = 2sin(		x + c) + 1
	2

to teraz wystarczy narysować funkcję

	π
y = 2sin(		x) + 1 i zobaczy o ile jest ona przesunięta w lewo od funkcji powyższej.
	2

ZKS: Przez powyższy wykres rozumiem ten co masz dany w zadaniu.