F.Kwadratowa cdn 2 Lukas: Funkcja y = (m + 1)x²−(2m+4)x−7 jest malejąca w zbiorze (− ∞ ;4) i rosnąca w zbiorze (4;+ ∞ ) . Wyznacz parametr m

	2
m=−		?
	3

razor: ok

Mila: Dobrze.

Lukas: Dla jakich wartości parametru m równanie mx² + 2x + m − 2 = 0 ma dwa pierwiastki mniejsze od 1?

razor: 1) m > 0, Δ > 0, f(1) > 0, x_w < 1 2) m < 0, Δ > 0, f(1) < 0, x_w < 1

Lukas: dwa przypadki jeśli ramionami do góry i drugi ramionami do dołu tak ?

razor: tak, można to było zapisać przy pomocy mniejszej ilości warunków ale nie pamiętam jak więc jest tak

Lukas: Dziękuję

ZKS: Można też od razu mf(1) > 0.

razor: o właśnie to

Lukas: mf ?

razor: m*f(1) > 0

ZKS: Jeżeli nie widać to wystarczy wymnożyć dla m > 0 oraz f(1) > 0 ⇒ m * f(1) > 0 i dla m < 0 oraz f(1) < 0 ⇒ m * f(1) > 0 stronami i otrzymamy jeden warunek m * f(1) > 0.

Lukas: Chyba jednak zostanę przy wersji razora.

Mila: Jakie dałeś warunki?

Lukas: Ja rozpatrzyłem tylko Δ>0 m>0 i f(1)>0 i drugi Δ>0 m<0 f(1)<0

Mila: 1) m≠0 wtedy x=1 2) Δ>0 m∊(1−√2,1+√2)\{0} 3) Aby nie rozważać dwóch przypadków mx²+2x+m−2=0 /:m

	2		m−2
x2+		*x+		=0
	m		m

f(1)>0 x_w<1

Lukas: Ale właśnie nie rozumiem wersji gdy sprawdzamy jeden przypadek przecież parabola może być ramionami do góry i ramionami do dołu ?

Mila: Ja sprowadziłam do jednego przypadku, a=1

Lukas: Ale chyba tak nie można ?

Mila: A dlaczego?

Lukas: Przecież nie można uogólniać przypadków do jednego ? Mnie uczono żeby rozważać dwie wersje.

Mila: Przeczytaj uważnie , co napisałam 20:40, masz wykluczone m=0. Po podzieleniu obu stron równania masz równanie równoważne. Wszystko jest w porządku, jesli jednak tego nie rozumiesz, to rozwiązuj swoim sposobem. Masz już dobry wynik?

Lukas: Mam dobry wynik, jednak chodzi mi o zrozumienie rozwiązania na jeden przypadek, takie rozwiązanie jednym sposobem mnie zgubiły w tym roku.

Mila: Konkretnie gdzie zastosowałeś taki skrót.

Lukas: I czemu trzeba badać jeszcze x_w<1 ?

Lukas: ?

Mila: Jeżeli wierzchołek paraboli leży na prawo od prostej x=1 i Δ>0 to conajmniej jeden z pierwiastków jest większy od 1.

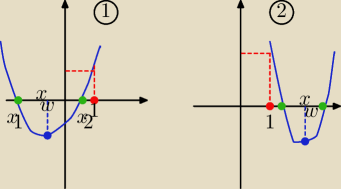
Eta: Widzisz dlaczego x_w musi być <1 ( na rys 1/ f(1)>0 ( na rys. 2/ też f(1)>0 ale x_w>1 który rys. spełnia warunki zadania?

Lukas: Ale tego rozwiązania sprowadzonego do jednego przypadku nadal ni w ząb, może jutro mnie olśnij, szkoda czasu teraz.

Lukas: 1 rysunek spełnia warunki zadania, ale ja ograniczyłem się tylko do Δ>0 i f(1)>0

Eta: Na pierwszym masz x_w<1 na drugim te same warunki ale x_w>1 −−− czyli nie spełnia warunku zadania zatem musisz jeszcze określić położenie wierzchołka : x_w<1

Mila: Właśnie miałam rysować.

Eta: Parametr musi spełniać trzy warunki : Δ>0 i f(1)>0 i x_w<1 Czy teraz już jasne?

Lukas: Teraz jasne, dziękuję. Tylko męczy mnie jeszcze drogie Panie przypadek podany przez Milę.

Mila: Zostaw go na późniejsze czasy. Na zakończenie działu.

Lukas: W sumie matura nie poszła mi tak źle bo z P mam 80%+ z moich wyliczeń

razor: Pisałeś w tym roku?

Lukas: Tak, ale tylko podstawę Na moją uczelnie nie dostanę się bo nie pisałem R i za późno się pokapowałem

Lukas: Razor a masz może zadania z funkcji kwadratowej z Pazdro ?

Piotr 10: ooo w Pazdro jest mase zadan z funkcji kwadratowej. Polecam

Lukas: Właśnie kończę zadanka z kiełbasy i robię jeszcze z zadania.info w między czasie żeby dobrze opanować dział.

Piotr 10: W Pazdro są fajne zadanka z funkcji kwadratowej ( trzymają wysoki poziom ).

razor: Jest tam 237 zadań na prawie 40 stronach więc nie wrzucę raczej wszystkiego naraz

Lukas: Nie musi być dziś, może być w weekend

Piotr 10: A nie lepiej kupić sobie ten zbiór od kogoś z byłych maturzystów za grosze ?

Lukas: Mam już chyba dosyć zbiorów a z Padzro tylko niektóre działy mnie interesują więc nie opłaca mi się kupować całego zbioru

razor: np. ode mnie

razor: https://www.dropbox.com/sh/ypnz6bm8ftoh1i6/AADuSQVqWOck2WZ6mHHgwiCoa masz zadania z parametrem narazie

Lukas: Danke !