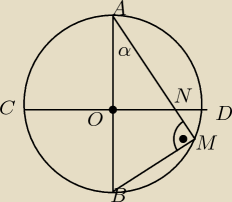
Okrąg godzio187: mam zadanie i nie wiem jak się za nie zabrać W okegu ośrodku O poprowadzono dwie prostopadłe średnice AB i CD. Z punktu A prowadzimy cięciwę AM przecinającą średnicę CD w punkcie N. Wyznacz miarę kąta, jaki cięciwa tworzy ze średnicą AB, jeżeli wiadomo, że czworokąt OBMN można wpisać okrąg.

godzio187: coś takiego zrobiłem a dalej to już nie wiem

godzio187: ABM −> α,90,90−α ABN −> α α β=180−2α BMN −> 90−2α , 90, 180−β=2α OBN −> 90, α, 90−α czyli ABM OBN jest przystający i tera co z tym MNB

Eta: 90^o − α

godzio187: Jedno pytanie, można wioskować że skoro BN=AN i <NMB = <AON to te trójkąty są przystające ?

AROB: α = 30⁰ Mam wyjaśnić, czy już doszedłeś?

godzio187: wyjaśnić

Eta: ze średnicą AB tworzy kąt α a ze średnicą CD tworzy kąt 90^o − α bo Δ AON jest prostokątny o kącie α

Eta: Ajjjj nie doczytałam zad. patrzyłam tylko na rys. godzia

godzio187: bo tam jeszcze ten okrąg można wpisać

AROB: Czworokąt OBMN musi być deltoidem , ponieważ kąty BON i BMN są proste, a sumy boków przeciwległych są sobie równe ( z warunku okręgu wpisanego w czworokąt). Stąd: IOBI = IBMI = r, IABI = 2r.

	IBMI		r		1
Z ΔABM : sinα =		=		=		⇒ α = 300
	IABI		2r		2

godzio187: o ! dzięki wielkie nie wiedziałem że ON = MN

godzio187: musze się ciągów pouczyć bo często się tu zdarzają a je bd mieć dosyć późno a utrwalać już se moge