wskazówka
mlepod: Na bokach AB, BC oraz AC trójkąta ABC, punkty a,b,c są obrane odpowiednio tak, że Ac= Ab, Ba=
Bc oraz Ca=Cb. Udowodnij, że punkty a,b,c są punktami styczności z okręgiem wpisanym w ten
trójkąt.Jakaś wskazówka
18 maj 23:49
Nieuchwytny: Narysuj rysunek

18 maj 23:53
mlepod:
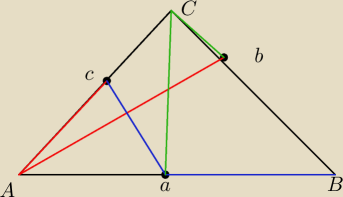
19 maj 00:00
mlepod:
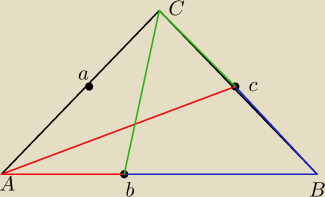
jeszcze ten mipasuje
19 maj 00:03
mlepod:
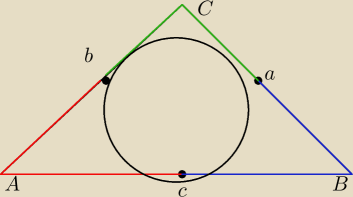
19 maj 00:09
mlepod: 
19 maj 00:16
mlepod: 
19 maj 00:29
mlepod: 
19 maj 00:39
mlepod: 
19 maj 00:53
PW: To proste: od dużego trójkąta zostały odcięte trzy trójkąty równoramienne. Dwusieczne kątów
tych trójkątów poprowadzone z wierzchołków A, B, C są jednocześnie symetralnymi podstaw cb, ca
i ab "małego" trójkąta. Ponieważ dwusieczne kątów wyznaczają środek okręgu wpisanego w trójkąt
ABC, a symetralne boków trójkąta abc wyznaczają środek okręgu opisanego na abc, i są to te
same proste, środek okręgu wpisanego w ABC jest środkiem okręgu opisanego na abc, co należało
wykazać.
19 maj 12:20


 jeszcze ten mipasuje
jeszcze ten mipasuje




