Anka: Prosze o pomoc w zadanku..Przekrój ostrosłupa prawidłowego czworokatnego, do ktorego nalezy przekatna podstawy i wierzchołek ostroslupa jest trojkatem rownoramiennym o polu S=12√3cm² i kacie przy podstawie alfa=30 stopni.Oblicz objetosc ostrosłupa..

M:

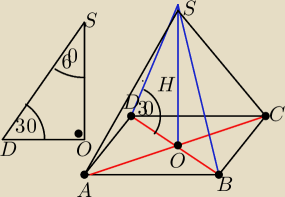
Mei Lin: Według mnie tym tym przekrojem będzie trójkąt równoramienny DBS |DB|=a√2 −przekątna podstawy

	1
|DO|=|OB|=		|DB|
	2

	a√2
|DO|=
	4

|∡BDS|=30^o |OS|=H −wysokość ostrosłupa i także wysokość trójkąta równoramiennego DBS . Trójkąt DOS jest trójkatem prostokątnym o kątach 30^o 60^o90^o

	|DO|
cos30o=
	|OS|

	|DO|
cos30o=
	H

	|DO|
H=
	cos30o

	a√2		2		a√2		a√6
H=		*		=		=
	2		√3		√3		3

Pole trójkata DSB P_DSB=12√3cm²

	1
Stąd pole trójkąta DOS PDOS=		PDSB=6√3cm2
	2

	1
PDOS=		*|DO|*|OS|
	2

1		a√2		a√6
	*		*		=6√3
2		2		3

a2√12
	=6√3
12

a²√12=72√3

	72√36
a2=		=36
	12

a=6 Podstawa jest kwadratem o boku dlugosci a=6

	a√6		6√6
H=		=		=2√6
	3		3

Objętośc ostrosłupa

	1
V=		*Pp*H
	3

	1
V=		*a2*H
	3

	1
V=		*36*2√6=24√6cm3
	3

Odp. Objętośc ostrosłupa jest równa 24√6cm³

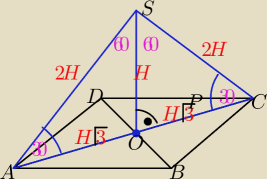
Hanka: ΔACS −−− przekrojem Z własności trójkąta "ekierkowego" o kątach ostrych 30^oi 60^o zaznaczam dane na rys. to: P(ACS)=12√3 H²√3=12√3 ⇒ H=2√3 d_p=|AC|=4√3

	d2
Pp=P□=		= 24
	2

	1
V=		Pp*H
	3

V= 16√3 =======

Anka: Mei Lin znowu zamula

Mei Lin: No dobra . Co jest złego w moim rozumowaniu oprócz tego ze nie wykorzystałem własnosci trójkata ekierkowego . Nie musze go znac moge sobie wyliczyc z funkcji trygonometrycznych . Pewnie takze gdzies sie pomyliłem ale to można znależc bład . Czas cenny na maturze ? Byc może

Hanka : Ja też poprawiam chochlika: d_p=|AC|=2H√3 = 12

	144
Pp=		=72
	2

V= 48√3 ======== Pozdrawiam Anka

Mei Lin:

Antoni: To fragment programu nauczania matematyki dla klasy 7. "Klasa 7 (115 h) 6. Trójkąty prostokątne (18 h) Twierdzenie Pitagorasa i jego zastosowanie do rozwiązywania zadań geometrycznych. Trójkąt prostokątny równoramienny i trójkąt o kątach 30°, 60°, 90°. Rozwiązywanie zadań geometrycznych z wykorzystaniem własności tych trójkątów."