PON ania122: proszę o pomoc jak ktoś wie jak to zrobić wyznacz równanie okręgu symetrycznego do okręgu o środku w punkcie O=(−2;6) i r=2 względam osi OX ; osi OY

Godzio: Odbij symetrycznie środek i napisz równanie Dla OX O'=(−2,−6), r = 2

ania122: jak odbić symetrycznie środek ? i jak do tego równanie napisać ?

Eta: O(−2,6) , r=2 O_OX(−2,−6) , r=2 o: (x+2)²+(y+6)²=4 O_OY(2,−6) , r=2 o: (x−2)²+(y+6)²=4

5-latek: https://matematykaszkolna.pl/strona/885.html

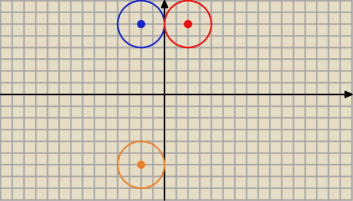
Eta: poprawiam zapis O_OY(2,6) , r=2 o: (x−2)²+(y−6)²=4

ania122: x² +4x +4 +y² + 12y +36= 4 x² +4x + +y² + 12y +36 = 0 to jest pierwsze równanie ? x² −4x +4 +y² + 12y +36=4 x² −4x + +y² + 12y +36=0 to jest drugie równanie ?

5-latek: jesli masz rownanie okregu w postaci kanonicznej to niee ma potrzeby (jesli o to nie prosza ) pisac je w postaci ogolnej