F.Kwadratowa
Lukas:
Znajdź te wartości parametru m, dla których funkcja f(x)=x2+mx+9ma dwa miejsca zerowe większe
od 2
Jakie założenia ?
Δ>0
x1>2
x2>2
18 maj 19:36
Lukas:
Nie pisać gotowych rozwiązań

18 maj 19:37
ZKS:
Pod względem matury Δ ≥ 0.
18 maj 19:49
Eta:
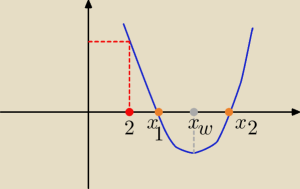
Δ≥0
f(2)>0
18 maj 19:54
Lukas:
Czemu tutaj f(2)>0 ?
18 maj 20:00
ZKS:
Masz rysunek przeanalizuj go. Jeżeli nadal nie rozumiesz to rób swoim sposobem.
18 maj 20:11
Eta:
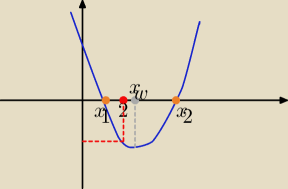
Parabola ramionami do góry , wierzchołek leży po prawej stronie liczby 2
i f(2)>0
kontrprzykład parabola ramionami do góry wierzchołek na prawo od liczby 2
i f(2) <0 ( wtedy obydwa miejsca zerowe
nie są większe od 2
18 maj 20:12
Lukas:
z wierzchołkiem rozumiem ale f(2)<0 ? może być tak ?
18 maj 20:25
Eta:
dla f(2)<0 −− masz na drugim rysunku....... odpada bo wtedy jedno z miejsc zerowych<2
zatem parametr m spełnia warunki: Δ≥0 i xw>2 i f(2)>0
Widzisz to na obydwu rysunkach? ( który spełnia warunki zadania? widzisz?
18 maj 20:39
Lukas:
Pierwszy rysunek spełnia warunki zadania.
18 maj 20:43
Eta:
Dokładnie tak

a na nim f(2) >0
18 maj 20:48
Lukas:
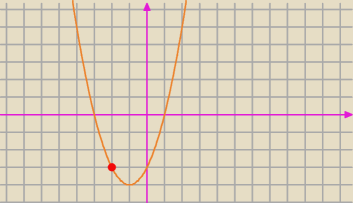
f(x)=x
2+2x−3
Ale wziąłem na konkretnym przykładzie i wychodzi że f(2)<0

18 maj 20:50
Lukas:
f(2)>0 przeprasza, źle spojrzałem.
18 maj 20:51
jakubs:
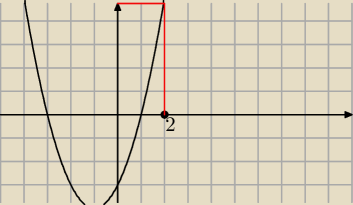
Na pewno f(2)<0 ?
18 maj 20:52
Lukas:
Patrz post wyżej

18 maj 20:54
ZKS:
Jeżeli współczynnik przy najwyższej potędze jest większy od 0 to ramiona paraboli skierowane są
do góry wtedy wartości dla argumentów pomiędzy miejscami zerowymi są ujemne. W zadaniu
mamy otrzymać dwa miejsca zerowe większe od 2 więc wartości nie mogą być ujemne dla
argumentu równego 2 ponieważ wtedy otrzymamy że te miejsca zerowe będą pomiędzy 2 czyli
jeden większy drugi mniejszy.
Bardziej tego rozpisać nie umiem.
18 maj 20:55
Lukas:
Już, zrozumiałem dziękuję

18 maj 20:56
ZKS:
To nie potrzebnie pisałem.
18 maj 20:57
Eta:

18 maj 20:57
Lukas:
Znajdź taką wartość parametru m ,aby największa wartość funkcji f(x)=−x2+mx+m była najmniejsza
z możliwych ?
Wartość największa yw funkcji ale jak zrobić aby była najmniejsza ? Tylko wskazówka jaki
warunek ?
18 maj 21:05
5-latek: Nastepny
Radek 
A tak nawiasem mowiac to ciekawe jak jemu poszlo bo sie nie odzywa
18 maj 21:07
Lukas:
Co złego, że w tym roku matura mi nie poszła i chcę się nauczyć do R ?
Proszę mnie do nikogo porównywać. A dwa co mi da gotowiec ?
18 maj 21:10
Eta:
| | −b | |
xmax= |
| to ymax=f(xmax |
| | 2a | |
g(m)=y
max −−−− osiąga minimum .... dokończ
18 maj 21:10
Lukas:
5−latek jak nie chcesz to nie musisz mi pomagać, ale komentarze tutaj są zbędne

18 maj 21:11
Eta:
Spokojnie
Lukas 
... bądź pokorny i grzeczny!
18 maj 21:12
kyrtap: Eta


18 maj 21:12
18 maj 21:12
jakubs: Jak ja się denerwuję to mi mama zawsze mówi " złość piękności szkodzi "

18 maj 21:14
Eta:
| | m2 | | m2 | |
g(m)= − |
| + |
| +m=.......... |
| | 4 | | 2 | |
18 maj 21:14
Lukas:
g(m) i co dalej ?
18 maj 21:15
pigor: ..., wskazówka ? proszę bardzo, jak wiesz zapewne W=(p,q), gdzie
p= −
b2a=
m2 ⇒ q=f(p)= f(
m2)= .... ile

= q(m)
i dopiero szukasz minimum g(m)= q
min dla m=

− szukany parametr m . ...

18 maj 21:15
18 maj 21:16
Eta:
Nie udziwniaj

18 maj 21:19
Lukas:
Nie udziwniam, po prostu tego nie rozumiem.
Wyznaczyłem f(xw) i klapki na oczach ?
18 maj 21:21
Eta:
| | m2 | | m2 | | 1 | |
ymax=f(xw)= − |
| + |
| +m= |
| m2+2 −−−− f. kwadratowa parabola ramionami |
| | 4 | | 2 | | 2 | |
do dołu więc osiąga minimum dla .....
18 maj 21:24
ZKS:
Z udziwnianiem chodziło zapewne to jak zapisałeś g(m). Zamiast zapisać
| | m2 | | −m2 + 2m2 + 4m | |
jak Eta czyli |
| + m to Ty zapisałeś |
| . |
| | 2 | | 4 | |
18 maj 21:25
Eta:
Dokładnie
ZKS 

18 maj 21:27
Lukas:
Ale dobrze chyba zapisałem ?
18 maj 21:27
pigor: ... , to raczej nie oznaczamy przez g tylko ku q,
a więc nie
12m
2+m jak u ciebie tylko :
q(m)=
14m
2+m=
14m(m+4) ⇒
⇒ q(m=
12(0−4))=q(
m=−2)= q
min; odp.
m=−2 . ...

18 maj 21:28
Eta:
| | 1 | | 1 | |
Ile to jest − |
| m2+ |
| m2=...... |
| | 4 | | 2 | |
18 maj 21:28
18 maj 21:30
Eta:
| | 1 | |
No tak f(xw)= |
| m 2+m ( znów chochlik  |
| | 4 | |
18 maj 21:30
pigor: 
to jak to jest

czy nie tak jak u mnie

; pozdrawiam i znikam

18 maj 21:30
18 maj 21:30
pigor: 
a jednak tym razem ...

18 maj 21:31
Eta:

18 maj 21:31
pigor: .., dlatego ja już wolę pisać jednak gotowce, bo może co ambitniejsza
i choć z minimum pokory młodzież, czegoś się zechce z nich nauczyć,
jeśli nie potrafi w spokoju uczyć się np. z podręcznika


..

18 maj 21:36
Lukas:
Dziękuję

18 maj 21:47
pigor: ... tez dziękuję ci
Lukasie i powiem ci, że wiem co mówię,
bo uczyłem się
sam na rozwiązanych przykładach w podręcznikach
i na rozwiązaniach "gotowcach" mądrych ludzi i tyle. ...

18 maj 21:54
Eta:
pigor dobrze gadasz , też tak uważam

( polać Ci ..........
pigwówki ?

18 maj 21:58
Lukas:
Ja wolę sam zrobić zadanie, a mądrych ludzi proszę o wskazówki jak do tego rozwiązania dojść

18 maj 22:04
pigor: oooo

kurcze jasne ; dziękuję; dziękuję baaaaardzo
Eta
właśnie już mój czas odejść od komputera czegoś się napić
−−−−−−−−−−−−−−−−−−−−
no cóż, powiem może tak :
ludzi warto się pytać o nieco inne rzeczy, a nie podstawowe

bo po prostu marnujesz ich czas i tyle .

, pozdrawiam
Lucasa,
18 maj 22:22
Lukas:
Mogę pytać o wszystko pigor, od tego to forum jest nawet o podstawowe rzeczy

Nikt nie karze
Ci ''marnować'' czasu przecież

Pozdrawiam.
18 maj 22:25
pigor: ,,, , tak też o myślałem i mam nadzieję, że znajdą się tacy
co ci pomogą z przyjemnością, ale ja

cóż, na pewno nie, bo
cenię sobie mój czas i moja pomoc nic by ci nie dała; dobrze ,
że choć w tym się dogadaliśmy, cieszę się, lubię to . ...

18 maj 23:14

 Δ≥0
Δ≥0
 Parabola ramionami do góry , wierzchołek leży po prawej stronie liczby 2
i f(2)>0
kontrprzykład parabola ramionami do góry wierzchołek na prawo od liczby 2
i f(2) <0 ( wtedy obydwa miejsca zerowe nie są większe od 2
Parabola ramionami do góry , wierzchołek leży po prawej stronie liczby 2
i f(2)>0
kontrprzykład parabola ramionami do góry wierzchołek na prawo od liczby 2
i f(2) <0 ( wtedy obydwa miejsca zerowe nie są większe od 2
 a na nim f(2) >0
a na nim f(2) >0
 f(x)=x2+2x−3
Ale wziąłem na konkretnym przykładzie i wychodzi że f(2)<0
f(x)=x2+2x−3
Ale wziąłem na konkretnym przykładzie i wychodzi że f(2)<0
 Na pewno f(2)<0 ?
Na pewno f(2)<0 ?



 A tak nawiasem mowiac to ciekawe jak jemu poszlo bo sie nie odzywa
A tak nawiasem mowiac to ciekawe jak jemu poszlo bo sie nie odzywa

 ... bądź pokorny i grzeczny!
... bądź pokorny i grzeczny!



 = q(m)
i dopiero szukasz minimum g(m)= qmin dla m=
= q(m)
i dopiero szukasz minimum g(m)= qmin dla m=  − szukany parametr m . ...
− szukany parametr m . ...





 to jak to jest
to jak to jest  czy nie tak jak u mnie
czy nie tak jak u mnie  ; pozdrawiam i znikam
; pozdrawiam i znikam 
 a jednak tym razem ...
a jednak tym razem ... 


 ..
.. 


 ( polać Ci .......... pigwówki ?
( polać Ci .......... pigwówki ? 

 kurcze jasne ; dziękuję; dziękuję baaaaardzo Eta
właśnie już mój czas odejść od komputera czegoś się napić
−−−−−−−−−−−−−−−−−−−−
no cóż, powiem może tak :
ludzi warto się pytać o nieco inne rzeczy, a nie podstawowe
kurcze jasne ; dziękuję; dziękuję baaaaardzo Eta
właśnie już mój czas odejść od komputera czegoś się napić
−−−−−−−−−−−−−−−−−−−−
no cóż, powiem może tak :
ludzi warto się pytać o nieco inne rzeczy, a nie podstawowe  bo po prostu marnujesz ich czas i tyle .
bo po prostu marnujesz ich czas i tyle .  , pozdrawiam Lucasa,
, pozdrawiam Lucasa,
 Nikt nie karze
Ci ''marnować'' czasu przecież
Nikt nie karze
Ci ''marnować'' czasu przecież  Pozdrawiam.
Pozdrawiam.
 cóż, na pewno nie, bo
cenię sobie mój czas i moja pomoc nic by ci nie dała; dobrze ,
że choć w tym się dogadaliśmy, cieszę się, lubię to . ...
cóż, na pewno nie, bo
cenię sobie mój czas i moja pomoc nic by ci nie dała; dobrze ,
że choć w tym się dogadaliśmy, cieszę się, lubię to . ... 