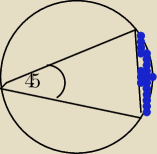
Trójkąt wpisany w okrąg myszka17: Równoramienny trójkąt ABC o kącie między ramionami 45stopni (rys) jest wpisany w okrąg o promieniu 8. a) oblicz długości łuków AB i BC b) oblicz pole zacieniowanego odcinka koła c) oblicz obwód trójkąta ABC

myszka17: kochani błagam, muszę mieć to jak najszybciej...a nie wiem jak się za to zabrać, wzór na pole wycinka tutaj jest bezwartościowy

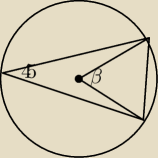
jakubs: Ile wynosi mara kąta β ?

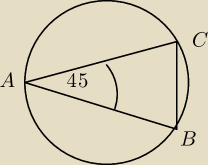
myszka17: No masz, faktycznie, ok, to już złapałam. Wyszło mi 4pi. (BC) Zapomniałam opisać. Ale jak obliczyć AB? i pozostałe dwa podpunkty.

razor: BC będzie 2π a nie 4π

razor: Żeby obliczyć łuk AB zauważ że jest on równy łukowi AC (dlaczego?) i razem z łukiem BC tworzą cały obwód. Zatem 2|AB| + |BC| = 16π

myszka17: W odpowiedziach widnieje: AB: 6π BC:4π l=(90+2π*16)/360=4π

razor: źle przeczytałem, faktycznie będzie 4π

myszka17: Są takie same, bo jest to trójkąt równoramienny, ok. Ale jak znalazłeś to 16π, bo nie zrozumiałam.

razor: 2πr − obwód

myszka17: No tak... Ok, podpunkt b) obliczyłam już z pola wycinka − pole trójkąta ze wzoru P=1/2ab*sinα, ale z podpunktem c) mam problem.

myszka17: odpowiedź to: 8(√2+√√2+2)

pigor: ..., na twoim rysunku długość : podstawy |BC|=8√2 ⇒ wysokość wzgl. niej h=|AE|= 8+4√2, a ramiona |AC|=|AB|= √(8+4√2)²−(4√2)²= √8*(8+8√2)= 8√1+√2, zatem Ob._ΔABC= 2|AC|+|BC|= 16√1+√2+8√2= 8(√2+√1+√2)....

d: tak piszecie ze nikt kto tego nie zrozumie XD

janek191: Odkopane po prawie 8 latach