pomoc
nata18: proszę o pomoc w tym zadaniu
Zaprojektowano plac na boisko sportowe w kształcie prostokąta.
Jednak, aby nie zniszczyć zadrzewienia postanowiono zmniejszyć długość projektowanego boiska o
30 metrów , a szerokość zwiększyć o 15 metrów . Otrzymano w ten sposób boisko kwadratowe o
polu stanowiącym 90 % pola boiska planowanego pierwotnie. Oblicz długość boku boiska
kwadratowego
18 maj 17:56
jakubs:
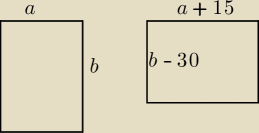
Oznaczę a i b jak w projekcie czyli pole P=ab
Pole po zmianach P
1=(a+15)(b=30)
0,9P=P
1
18 maj 18:58
nata18: akurat do tego momentu sama doszłam tylko co dalej tylko zamiast a i b dałam x i y
18 maj 19:00
kochanus_niepospolitus:
jak to co ... układ równań i rozwiązujesz
18 maj 19:01
kochanus_niepospolitus:
b−30 = a+15 (bo to ma być kwadrat)
a*b*0,9 = (b−30)*(a+15)
i rozwiązujesz ten prosty układ równań
18 maj 19:02
nata18: układ równań rozumiem

tylko jaki tu początek ma być ty układów to później już sobie poradzę obliczyć tak myślę

18 maj 19:03
nata18: a to rozwiąże go tu i sprawdzisz czy dobrze rozwiązany zostanie ?
18 maj 19:04
kochanus_niepospolitus:
nie ma problemu
18 maj 19:05
jakubs: Przepraszam tam u mnie w nawiasie oczywiście powinno być (b−30).
18 maj 19:06
nata18: b−30 = a+15
a*b*0,9 = (b−30)*(a+15)
b = a+45
9/10 ab = ab+ 15b − 30a−450
18 maj 19:07
nata18: dobrze do tego mometu mam
18 maj 19:08
kochanus_niepospolitus:
nom ... i co dalej

18 maj 19:08
nata18: a+45−30 = a + 15
9 ab = 10 ab +150b − 300a − 4500
0 = 0
−1 ab = 150b − 300a − 4500
1 ab = 300a − 150b + 4500
18 maj 19:12
kochanus_niepospolitus:
a+45−30 = a + 15 <−−−− po co to

w pierwszym równaniu masz b= a+45
podstaw (b) do drugiego równania
9a(a+45) = .... itd. .....
18 maj 19:14
nata18: 0 = 0
b = 300 − 150b + 4500
0=0
151b = 4800
18 maj 19:15
kochanus_niepospolitus:
dlaczego przyjęłaś, że a=1

18 maj 19:16
nata18: b = a+45
9/10 a * (a+45) = a a+45+ 15 8 (a+45) − 30a−450
18 maj 19:16
nata18: tak ma być podstawione ?
18 maj 19:17
kochanus_niepospolitus:
tak
po wymnażaj ... wszystko na jedną stronę i masz wielomian kwadratowy
liczysz Δ
18 maj 19:17
nata18: 40,5a +a2 = a2 +45a + 15a + 675 − 30 a − 450
18 maj 19:20
nata18: 10,5a −225 = 0
18 maj 19:21
kochanus_niepospolitus:
może ... rozwiązuj ... czekam na konkretne wyniki
18 maj 19:21
kochanus_niepospolitus:
co

a w życiu

18 maj 19:21
nata18: to nie wiem kurcze gdzie błąd jest
18 maj 19:22
kochanus_niepospolitus:
| 9 | |
| a*(a+45) = a*(a+45) + 15*(a+45) − 30a − 450 |
| 10 | |
| | 1 | |
− |
| (a2 + 45a) = 15a + 675 − 30a − 450 |
| | 10 | |
| | 1 | |
− |
| (a2+45a) = −15a + 225 |
| | 10 | |
−a
2 − 45a = −150a + 2250
−a
2 + 105a − 2250 = 0
18 maj 19:23
nata18: Δ = 11025 − 4 * (−1) * (−2250)
Δ = 25
√Δ = 5
18 maj 19:26
nata18: i co dalej
18 maj 19:26
jakubs: wyznaczasz a
18 maj 19:26
kochanus_niepospolitus:
no i policz a1 i a2
a następnie do wiliczonego a1 wyznacz b1 ... do a2 wyznacz b2
później sprawdź czy takie pary liczb spełniają warunki zadania
18 maj 19:27
nata18: z czego wyznaczyć a ?
18 maj 19:27
nata18: a to wiem już dokończe sama dziękuje wam za pomoc
18 maj 19:28
nata18: a1 = 150−5/−2
a1 = 72,5
a2 = 150 +5 / −2
a2 = 77,5
b1 = a1+45
b1= 72,5 + 45
b1 = 117,5
b2 = a2+45
b2 = 77,5 + 45
b2 = 122,5
a1 = 72,5
b1 = 117,5
a2 = 77,5
b2 =122,5
117,5 − 30 = 87 ,5
72,5 + 15 = 87 ,5
mamy kwadrat
122,5 − 30 =92,5
77,5 + 15 = 92,5
też mamy kwadrat
2 rozwiązania są
18 maj 20:40
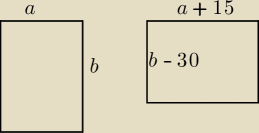 Oznaczę a i b jak w projekcie czyli pole P=ab
Pole po zmianach P1=(a+15)(b=30)
0,9P=P1
Oznaczę a i b jak w projekcie czyli pole P=ab
Pole po zmianach P1=(a+15)(b=30)
0,9P=P1
 tylko jaki tu początek ma być ty układów to później już sobie poradzę obliczyć tak myślę
tylko jaki tu początek ma być ty układów to później już sobie poradzę obliczyć tak myślę 

 w pierwszym równaniu masz b= a+45
podstaw (b) do drugiego równania
9a(a+45) = .... itd. .....
w pierwszym równaniu masz b= a+45
podstaw (b) do drugiego równania
9a(a+45) = .... itd. .....

 a w życiu
a w życiu 