prawdopodobieństwo tyu: Proszę o sprawdzenie zadania Ze zbioru Z={ x∊ N: 4^x−4 * 0,5^5−x < 2^x−3 * 4 ^6/x } losujemy kolejno ze zwracaniem dwie liczby. Oblicz prawdopodobieństwo, że ich suma jest większa od 8.

	6
wykładnik "6/x" to jest ułamek		ale jakiś niewyraźny zapis był przy pomocy kodu
	x

		, więc zapisałem to jako "6/x"

Rozwiązanie jest tutaj http://www.matematyka.pl/117706.htm ale chyba tam jest błąd w obliczeniu rozwiązań, bo na koniec wychodzi mi inny przedział niż podany w linku 2x² − 10x − 12< 0 zatem a=2, b=−10, c=−12 Δ=196=14²

	10−14		−4		10+14		24
x1=		=		= 1 x2=		=		= 6
	4		4		4		4

czyli x∊(−1,6) i x∊N => x∊{1,2,3,4,5} chyba tutaj nie wpisuję zera ? IΩI = 5² W linku jest też inna moc Ω, która wynosi IΩI = 4²=16, więc wynik nie może być

	3
prawidłowy, bo prawidłowe prawdopodobieństwo to P(A) =
	25

więc pary spełniające warunek to (4,5) (5,5) (5,4)

	3
P(A) =		wynik jest dobry, ale nie wiem, bym szukał tych trzech par, ale np cztery
	25

pary, nie znając wyniku czy ktoś mógłby mi to sprawdzić, bo nie wiem, czy się gdzieś nie pomyliłem. Sam się tego uczę, w podręczniku jak zwykle są tylko najprostsze przykłady.

sushi_ gg6397228: zapisz po kolei obliczenia zbioru "Z", a nie ostateczną postać

tyu: czyli chodzi Ci jak rozwiązałem funkcję wykładniczą ?

sushi_ gg6397228: tak

tyu: 2^2(x−4) * 2^−(5−x) < 2^x−3 * 2^12/x 2^2x−8+x−5 < 2^x−3+12/x 2^3x−13 < 2^x−3+12/x

	12
3x−13< x−3+
	x

	12
2x−10 −		< 0 / * x
	x

2x²−10x − 12< 0 resztę już napisałem wyżej

sushi_ gg6397228:

	12
2x− 10 −		<0
	x

jeżeli nie mamy treści zadania tylko takie coś, to nie możemy pomnożyć nierownosci przez "x", bo nie wiemy jakiego jest znaku−−> trzeba zrobic wspolny ułamek jak w linku

2x2− 10x − 12
	<0 / * x2
x

x* (2x²− 10x − 12) <0 potem sa trzy miejsca zerowe, fala , przedział + założenia x≠0 bo pomyliła sie w obliczeniach M.Z.

tyu: okej, rozumiem, ale tam jest chyba źle obliczony X₁. Tak jak wyżej napisałem mi wychodzi, że to jest x₁=−1, a nie jeden. Czy mógłbyś sprawdzić jeszcze ten aspekt, bo wszystko inne się mi zgadza. W rozwiązaniu w linku moc omegi jest za mała (16). Żeby omega była prawidłowa (25), to jedynka musi należeć do zbioru Z − tak mi się wydaje.

sushi_ gg6397228: napisałem w ostatniej linijce " pomyliła, się w obliczeniach MZ−−> miejsca zerowe" x₁=−1, x₂=0, x₃= 6

tyu: aha, nie zrozumiałem tego. Dziękuję za pomoc.

PW: Zaraz, zaraz, w treści zadania było: x∊N − dlaczego nie można pomnożyć przez dodatnie x?

tyu: dobre pytanie, bo x∊N, więc chyba można ?

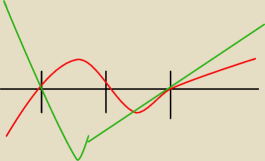
sushi_ gg6397228: teraz patrz na rysunki, czy w każdym przedziale "kolory" są tego samego znaku ?

PW: Ale ja pytałem nie dlatego, że nie wiem, tylko dlatego, że Ty nie wiesz. Dziedziną nierówności

	12
2x − 10 −		< 0
	x

w tym zadaniu są liczby dodatnie, i to położone "rzadko" − tylko liczby naturalne. Jaki jest sens rozważania nierówności dla wszystkich x rzeczywistych, rysowania wykresów? Żeby się narobić, czy żeby pokazać niezrozumienie treści zadania?