proste 5-latek: Witam. Moge prosic o narysowanie tych dwoch sytuacji . 1. W ilu punktach przrcinaja sie 4 proste rozne gdy kazda przcina wszystkie pozostale przy czym przez zaden punktow przeciecia nie przechodzi wiecej niz dwie proste . 2. Obieramy 5 roznych prostych . W iulu co najwyzej punktach przecinaja sie te proste . Reszte zadan z tego paragrafu rozwiazalem . dzieki za pomoc .

5-latek: napewno 5 roznych prostych przetnie sie w jednym punkcie to wiem

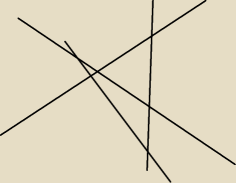
math.h: to pierwsza sytuacja (6 punktów)

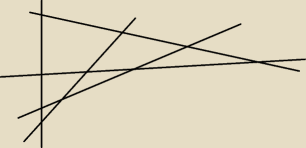
math.h: dla 5 prostych − 10 punktów

5-latek: Zaraz to przetrawie

5-latek: A do drugiej moze byc tak ? Bedzie w 4 punktach . Te kolorowe sa do siebie rownolegle ?

math.h: ale masz w ilu NAJWIĘCEJ punktach może się przeciąć 5 prostych. A jak żadne dwie nie sią równoległe, to punktów przecięcia bedzie więcej

5-latek: Wiesz ale tam pisze w ilu co najwyzej

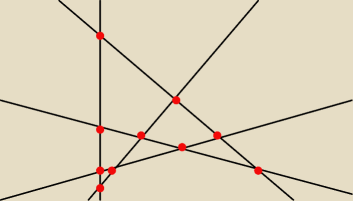
Trivial: Każda prosta przecina się z każdą inną. Lepiej być nie może.

Trivial: Cztery proste analogicznie. Liczbą przecięć jest po prostu

	(n−1)n
1 + 2 + 3 + ... + (n−1) =		.
	2

5-latek: Dziekuje . czyli tak jak kolega wyzej napisal

5-latek: Zaczynam sie uczyc geometrii (dla klasy 1 technikum W Janowski i tam sa takie zadania . Wiec chcialbym to od poczatku zrozumiec dlatego zadaje te pytania .

PW: To jest to samo zadanie, co o powitaniach na przyjęciu. Jeżeli na przyjęciu jest n osób i każdy wita się z każdym, to uścisków rąk jest

	n 2		n(n−1)
(1) r =		=		.
			2

Ze zbioru n prostych wybieramy wszystkie możliwe 2−elementowe podzbiory i przyporządkowujemy im ich punkt wspólny. Jeżeli żadna z par nie jest parą prostych równoległych i żadne różne pary nie przecinają się w tym samym punkcie, to liczba wspólnych punktów jest określona wzorem (1). Więcej wspólnych punktów być nie może, gdyż zgodnie z odpowiednim aksjomatem dwie różne i nierównoległe proste mają tylko jeden punkt wspólny. Rozwiązanie nie wymaga rysunków ani rozstrzygania, czy to w ogóle jest możliwe, gdyż pytanie brzmi "ile co najwyżej ..."

5-latek : Dziekuje PW Mysle jednak z erysunek jest tu potrzebny gdyz uczen 1 klasy techniku nie zna symbolu Newtona . Moj blad polegal na tym ze jak przyjalem ze to ma byc ilosc najmniejsza .

PW: Jasne, ale ja wiem, że nie jesteś uczniem pierwszej klasy technikum, który może to policzyć elementarnie − jak to sugerował Trivial Najważniejsze w rozumowaniu jest przywołanie aksjomatu − więcej być nie może, bo dwie różne proste mają co najwyżej jeden punkt wspólny (gdzieś tam daleko poza kadrem rysunku nie "zakręcą" i nie spotkają się ponownie).

aga: Proszę o pomoc . Ile punktów wspólnych ma 10 prostych, które żadne 2 nie są równoległe i żadne 3 nie przecinają się w jednym punkcie