czworokąty
Frank: Siema
Mam problem z następującym zadaniem. Podpunkt a, zrobiłem nie umiem b.
Wysokości równoległoboku wynoszą 2.4 cm i 4cm, a jego obwód jest równy 16cm.Oblicz
b) cosinus kąta rozwartego między przekątnymi tego równoległoboku.
Długości boków z a mi wyszły 5 i 3. Chciałem to zrobić z twierdzenia cosinusów, ale nie wiem
jak wyznaczyć przekątne.
17 maj 20:48
sushi_ gg6397228:
wzór na pole równoległoboku .....
17 maj 20:52
Frank: nie czaję
17 maj 21:18
Eta:
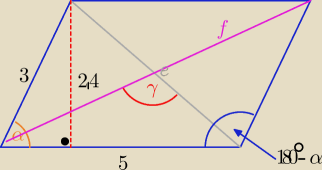
| | 2,4 | | 4 | | 3 | |
sinα= |
| = |
| , to cosα= |
| |
| | 3 | | 5 | | 5 | |
e,f >0
Z tw. kosinusów :
| | 3 | |
e2=52+32−2*5*3* |
| ⇒ e=....... |
| | 5 | |
| | 3 | |
f2=52+32+2*5*3* |
| ⇒ f=.... , ( cos(180o−α)= −cosα |
| | 5 | |
| | (0,5e)2+(0,5f)2−a2 | |
cosγ= |
| = ........ ( cosγ<0 , bo γ−− kąt rozwarty |
| | 2*0,5e*0,5f | |
dokończ obliczenia
17 maj 22:12
krystek:
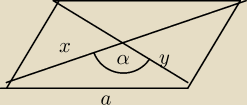
a
2=x
2+y
2−2xycosα
17 maj 22:14
Eta:
Witaj
krystek 
17 maj 22:16
Frank: Już mi się objaśniło. Tylko skąd wzór na cos y ?
17 maj 23:02
kyrtap: Z tw. cosinusów :
5
2 = (0,5e)
2+(0,5f)
2 − 2* 0,5e *0,5f * cosγ
2* 0,5e *0,5f * cosγ =(0,5e)
2+(0,5f)
2 − 5
2 / : (2* 0,5e *0,5f )
| | (0,5e)2+(0,5f)2 − 52 | |
cosγ= |
| |
| | 2* 0,5e *0,5f | |
17 maj 23:13