Parabola
Lukas:
200/52 A.Kiełbasa
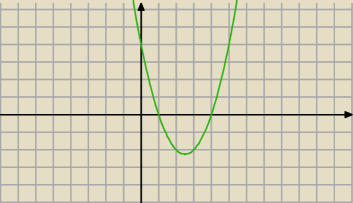
korzystając z wykresy funkcji f(x)=ax
2+bx+c określ znak liczby:
1).a
czy wystarczy taka odpowiedź ramiona paraboli skierowane są do góry dlatego współczynnik a>0 ?
17 maj 18:19
jakubs: Według mnie tak.
17 maj 18:20
J: Tak... bo tylko a decyduje o zwrocie ramion paraboli
17 maj 18:23
Lukas:
Wiem, że a decyduje o tym ale chodziło czy poprawnie matematycznie
2) b ?
jak określić jakie jest b ?
17 maj 18:24
Mila:
Wystarczy.
17 maj 18:26
J:
Jakiego znaku jest xw wierzchołka ?
17 maj 18:26
17 maj 18:27
J:
17 maj 18:28
jakubs: | | −b | |
Pierwsza współrzędna wierzchołka paraboli oznaczmy xw= |
| |
| | 2a | |
Wiesz, że x
w >0 i a>0, tak więc jaki wniosek ?
17 maj 18:28
Lukas:
3) c punkt przecięcia z osią OY c>0
17 maj 18:29
jakubs: 
17 maj 18:30
J: Tak.. bo f(0) = c
17 maj 18:31
Lukas:
4) a2−bc ?
a>0
b<0
c>0
a2−bc>0
17 maj 18:33
J: Tak ... bo: − bc > 0
17 maj 18:37
Lukas:
b2−ac
Tutaj nie wiadomo ?
tutaj wszystko pasuje ?
17 maj 18:42
Mila:
Δ>0, bo są dwa miejsca zerowe⇔
b2−4ac>0, wiemy , że ac>0 w takim razie
b2−ac>b2−4ac>0 (mniej odejmujemy)
17 maj 19:06
Lukas:
Czyli w taki sposób
17 maj 19:17
Lukas:
5.17
Wyznacz wszystkie wartości parametru k∊R, aby liczba 2 znajdowała się między miejscami zerowymi
funkcji f(x)=x2+4x+k
Jakie założenia
Δ>0
?
17 maj 20:14
jakubs: f(2)<0
17 maj 20:20
Lukas:
Czemu f(2)<0 ?
17 maj 21:33
jakubs: Parabola skierowana ramionami do góry, więc pomiędzy miejscami zerowymi funkcja przyjmuje
wartości ujemne. Liczba 2 ma być między miejscami zerowymi, więc f(2)<0.
17 maj 21:36
Lukas:
x1<2
x2>2
?
17 maj 21:53
jakubs: Według mnie będą 2 założenia 1 które podałeś czyli Δ>0 i f(2)<0.
Δ=16−4k
16>4k
4>k
f(2)=4+8+k<0
12<−k
−12>k
odp: k<−12
Niech się lepiej ktoś mądrzejszy wypowie, żeby nie okazało się że wprowadzam w błąd.
17 maj 21:56
Eta:
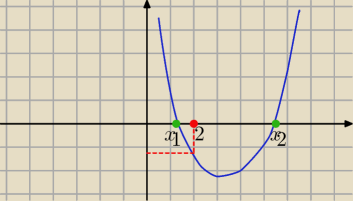
1/ Δ>0
2/ f(2) <0
17 maj 22:15
Lukas:
Mam rysunek, ale nie wiem czemu f(2)<0 ?
17 maj 22:19
jakubs: Czytałeś mój post z 21:36 ?
17 maj 22:33
Lukas:
Czytałem.
17 maj 22:35
jakubs:
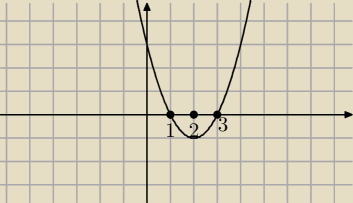
Dajmy taki przykład:
Jakie będzie f(2) ?
17 maj 22:37
jakubs: W sensie f(2)>0 czy f(2)<0 ?
17 maj 22:38
Lukas:
f(2)<0 ale jaki to ma związek z miejscami zerowymi ?
17 maj 22:39
jakubs:
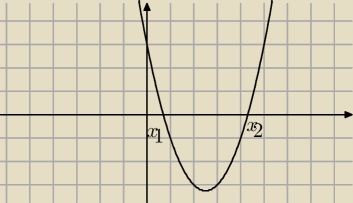
Jeżeli ramiona paraboli są skierowane w górę to dla dowolnego x, który leży między x
1 a x
2,
funkcja będzie przyjmowała wartości ujemne.
17 maj 22:43
Lukas:
Dziękuję, zrobione w końcu
18 maj 16:47
Lukas:
a jeśli funkcja f(x)=−x2+4x+k to wtedy f(2)>0
18 maj 19:03
jakubs: Tak
18 maj 19:04