funkcja aś: Przedziały wklęsłości/wypukłości funkcji.

	2x(1−x2)2+4x(1−x2)(x2+1)
jak je obliczyc gdy mam f ''(x)=
	(1−x2)4

wiem ze f ''(x)=0 i dla f''(x)>0 jest wypukła a f''(x)<0 wklęsła.

kochanus_niepospolitus: badasz znak mianownika

kochanus_niepospolitus: tfu ... licznika bo mianownik >0

kochanus_niepospolitus: 2x(1−x²)² + 4x(1−x²)(x²+1) = (1−x²)*(2x+ 4x*(x²+1)) = (1−x²)*2x*(1 + 2*(x²+1)) = = (1−x²)*2x*(2x²+3) no i jakie masz miejsca zerowe w drugiej pochodnej

aś: no ok i dochodze do momenty gdy: 6x−4x³−2x⁵=0 czyli 2x(3−2x²−x⁴)=0 i jak to dalej doprowadzic do postaci zeby byly ladne miejsca zerowe?

kochanus_niepospolitus: skopałem −−− 2x(1−x²)² + 4x(1−x²)(x²+1) = (1−x²)*(2x(1−x²)+ 4x*(x²+1)) = .... 'ciągnij dalej'

kochanus_niepospolitus: niepotrzebnie wymnażasz (1−x²) ... patrz co ja mam

aś: ehh.. nigdy nie bylam dobra w tym "wyciaganiu" wspolnych czesci

aś: czyli 2x(1−x²)(2x³+x²+1)

aś: pewnie cos pomylilam

aś:

J: Źle.. jak wyciagasz 2x , to po co mnożysz ostatni nawias przez 2x ?

aś: nie wiem to jak to powinno byc?

J: = 2x(1−x²)[(1−x²) +2(x²+1)] = 2x(1−x²)(1 − x² +2x² + 2) = = 2x(1−x²)(x²+3)

aś: czemu 1−x²+2x²+ 2 a nie +2x

aś: aaaa dooobra juz widze moj blad

aś: czyli x={0,−1,1,−√3,√3} tak?

aś: ale czy teraz musze odrzucić −1 i 1 bo w mianowniku bylo (1−x²)⁴

J: Popatrz na nawias kwadratowy ..... po wymnożeniu i uporzadkowaniu mamy: x² + 3

J: Skąd masz: − √3 oraz √3 ?

aś: ah faktycznie tam bedzie x²=−3 czyli pozostaje tylko 0

kochanus_niepospolitus: J ... no przecież x²+3 = 0 −> x² = −3 −> x = −√3 lub x=√3

J: Tak... bo −1 oraz 1 nie należą do dziedziny

J: Racja "kochanus" .... nie pomyślałem ...

aś: czyli ze f jest wypukla gdy x∊(−∞,0)? a wklesla dla x∊(0,+∞)

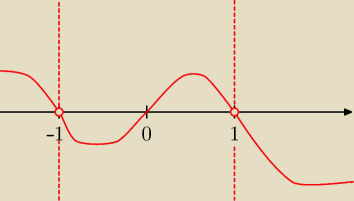
kochanus_niepospolitus: tak ... i nie szkic f''

aś: czyli?

kochanus_niepospolitus: tak −−− −1 i 1 NIE BĘDĄ punktami przegięcia (bo nie należą do dziedziny) nie −−− 'znak' (1−x²) zależy właśnie od tego po której stronie jesteśmy tych punktów ... i trzeba je ując (miejsca zerowe) na szkicu wykresu f''(x)

kochanus_niepospolitus: co czyli co miałaś rysowanie szkiców wykresów f' i f''

aś: nie mialam. czyli dla jakich przedzialow bedzie wypukla a dla jakich wklesla i jaki bedzie punkt przegiecia

kochanus_niepospolitus: zapoznaj się z tematem: https://matematykaszkolna.pl/strona/1692.html następnie samodzielnie narysuj taki sam szkic co ja następnie na podstawie szkicu napisz kiedy funkcja jest wklęsła a kiedy wypukła.

aś: czyli wypukla dla x∊(−∞,−1) i (0,1) a wklesla dla (−1,0) i (1,+∞) w punktem przegiecia bedzie tylko 0?

aś:

J: Tak

aś: dziekuje bardzo za pomoc