Trapez o obwodzie 26 Karolina_96: Bardzo proszę o rozwiązanie tego zadania Dany jest trapez o obwodzie 26cm, jego trzy boki są takie same a wysokość jest równa 4cm. Oblicz pole i przekątną tego trapezu.

Piotr 10: Jeżeli trzy boki są równe to znaczy, że jest to trapez równoramienny oraz. ze przekątne sa dwusiecznymi kątów.

Karolina_96: no dobrze, ale co dalej?

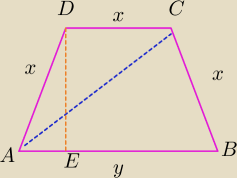
Piotr 10: 3x+y=26 y=26 − 3x

	y−x		26 −3x −x		26 − 4x
IAEI =		=		=		=13 − 2x
	2		2		2

Teraz z tw. Pitgarasa dla ΔAED x²=4²+(13−2x)² Dalej poradzisz sobie sama ?

Karolina_96: postaram się dzięki

pigor: ..., np. niech ABCD dany trapez i E − spodek wysokości DE i |DE|=4, to jeśli |AB|=a i |AD|=|CD|=|BC|=r, |BD|=? −szukana przekątna i P_t= ¹₂(r+a)*4= 2(r+a)=? , ale 3r+a=26, to a=26−3r , wtedy P_t= 2(r+26−3r)=2(26−2r)= 4(13−r)=?− szukane pole, −−−−−−−−−−−−−−−−−−−−−−−−−−− ale |AE|= ¹₂(a−r)= ¹₂(26−3r−r)=13−r i z ΔADE: |AD|²+4²=r² ⇔ (13−r)²−r²+16=0 ⇔ 13²+r²−26r−r²+16=0 ⇔ ⇔ 26r=169+16 ⇔ r= ¹⁸⁵₂₆= 7,1153 , więc P_t= 4(13−7,1153)= 4*5,8846= 23,5384 −−−−−−−−−−−−−−−−−−−−−−−− natomiast : BD²= 4²+BE²= 16+5,8876²= 50,6285 ⇒ ⇒ |BD|=7,1154 − szukana długość przekątnej trapezu . ... −−−−−−−−−−−−−−−−−− wyniki nie ciekawe, więc radzę mnie sprawdzić, czy gdzieś się nie ...