liczby zespolone Bartek: Narysować zbiory liczb zespolonych z spełniających podane warunki:

π
	< arg (z3) < π
2

Ponieważ arg (z³)=3*argz Wyszło mi coś takiego:

π
	<3*argz + 2kπ<π /:3
2

π		2kπ		π		2kπ
	−		< argz <		−
6		3		3		3

W rozwiązaniu jest podane coś czego nie rozumiem. Dlaczego oni piszą, że: 0≤argz<2π oraz piszą,że moja nierówność ma sens tylko dla k∊{0,−1,−2} ?

Bartek: No to ja odświeżam.

Bartek: To ja jeszcze poproszę o wytłumaczenie tutaj.

Bartek: Czy mógłbym po prosić pomoc? Po prostu nie rozumiem wniosku z rozwiązania tego zadania.

Bartek: Sory, czy może ktoś mi pomóc jeszcze w tym zadaniu. Bo tak już ze 3 dni czekam.

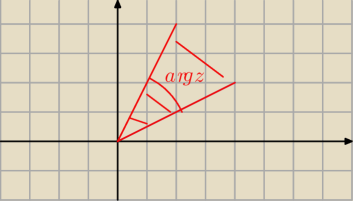
Krzysiek: arg(z³)=3argz więc masz: π/6<argz<π/3 http://pl.wikipedia.org/wiki/Argument_liczby_zespolonej I nie wiem czemu ktoś pisze,że nierówność ma sens tylko dla k∊{0,−1,−2} co najwyżej możesz napisać π/5+2kπ<argz<π/3+2kπ tyle,że arg(z) jest zdefiniowany jako kąt należący do przedziału [0,2π) więc te '2kπ' już nie dopisujesz.

Mila: 0≤argz<2π taką masz definicję argumentu głównego liczby zespolonej. k należy tak dobrać, aby ten warunek był spełniony k=0

π		π
	<arg(z)<		zgadza się
6		3

dalej sam sprawdź. Obejrzyj> http://www.youtube.com/watch?v=d3I_gaZ3oK8

Bartek: Dziękować