Dziedzina funkcji dyzio: Wyznacz liczbę a, dla której dziedziną funkcji f jest podany obok wzoru funkcji zbiór D_f

	1
f(x)= √x + 4 +		Df = <−4 , 1) ∪ (1 , +∞)
	x + a

	x − 1
f(x)=		Df = R − {−6 ; 2}
	|x + 2| + 3a

	x − 1
f(x)=		Df = (−∞ ; −6) ∪ (10 ; +∞)
	√|2 − x| − 2a

Jakby ktoś mógł pomóc mi w zrozumieniu tego typu zadań byłbym wdzięczny.

Marcin: |x + 2| + 3a =0, skoro z dziedziny odpadają liczby −6 i 2, to

	4
4+3a=0 ⇒ 3a=−4 ⇒ a=−
	3

	4
i |−6+2|+3a=0 ⇒ 4+3a=0, co też prowadzi do a=−
	3

dyzio: Z konkretnymi wartościami w D_f w miejsce x podstawiamy te liczby co odpadają z dziedziny tak ? Analogicznie robi się inne tego typu zadania ? Dobrze rozumiem ? A co z z przedziałami ?

Marcin: w pierwszym masz od razu założenie, że x+4>0, więc x>−4, teraz musisz jeszcze wyrzucić jedynkę z dziedziny. 1+a=0 ⇒ a=−1

dyzio: OK, w pierwszym przykładzie widać, że mamy 1 wyrzucić a co z trzecim przykładem ? Tam już mamy większy wybór liczb?

Marcin: |2−x|−2a>0 |2−x|>2a Teraz pomyśl chwilę sam, co można wstawić za a

dyzio: − 6 i 10 ?

dyzio: |2−(−6)| = 2a 8 = 2a a = 4 |2− 10| = 2a 8 = 2a /2 a = 4 Dobrze ?

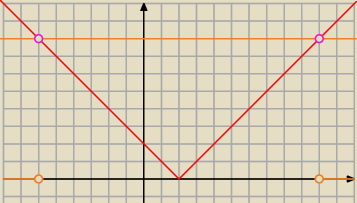
Marcin: Podpowiedź graficzna

Marcin: Tak, dobrze Nie zauważyłem tego wpisu

dyzio: Ok dzięki za wytłumaczenie

Marcin: No problem