Wartośc bezwzględna Radek: Wartość bezwzględna. Witam mam taki przykład. |x²−9|−|x²−4|=5 Z pierwszego wyszło: x∊(−∞,−3>∪<3,∞) Z drugiego wyszło: x∊(−∞,−2>∪<2,∞) Więc w jakich przedziałach rozwiązuje te równanie ? Dziękuje za pomoc

J: A skąd Ci wyszło z pierwszego ... x ∊ .... ?

Radek: x²−9≥0 (x−3)(x+3)≥0 x=3 ⋁ x=−3 x∊(−∞,−3>∪<3,∞)

Marcin:

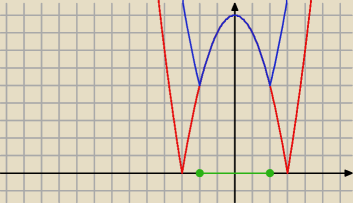
J: A ... chodziło o przedziały rozwiązywania .. to masz ich 5: (−∞,−3) <−3,−2) <−2,2) <2,3) <3,+∞) Albo graficznie: Ix² − 9I = Ix² − 4I + 5

J: No właśnie ..

Radek: Rozumiem, a od czego zależy to czy w tych przedziałach są te nawiasy domknięte czy otwarte ?

J: Domykasz tak, aby ne "zgubić" żadnej wartości ...

Radek: Hmyy wyszło mi rozwiązanie tylko x=2\\ 1.(−∞,−3) −x²−9+x²−4=5 Brak 2.<−3,−2) −x²+9−x²+4=5 x=2 i x=−2 Nie jest rozwiązaniem w tym przedziale 3.<−2,2) −x²−9+x²−4=5 Brak 4.<2,3) −x²+9−x²+4=5 x=2 i x=−2 Więc 2 jest rozwiązaniem 5.<3,+∞) x²−9−x²+4=5 Brak Więc gdzie jest błąd ?

PW: A nie wiem, czy nie można zrobić tego mniejszym wysiłkiem. Mamy sytuację |a| − |b| = 5 przy założeniu, że a − b = − 5. Rzeczywiście, dla dowolnej x∊R jest x² − 9 − (x² − 4) = − 5. Pytają więc − kiedy |a| − |b| = 5 = |−5| = | a − b |. Czy wiadomo dla jakich a i b |a| − |b| = | a − b | ?